Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Derivada Exponencial e Logarítmica

Ver Todos os Exercícios

Teoria

Opa, seja muito bem vindo ao Responde Aí! Bora bater um papo sobre derivada exponencial e logarítmica?

Derivada Exponencial

Para calcular a derivada de uma função exponencial, usamos a seguinte fórmula:

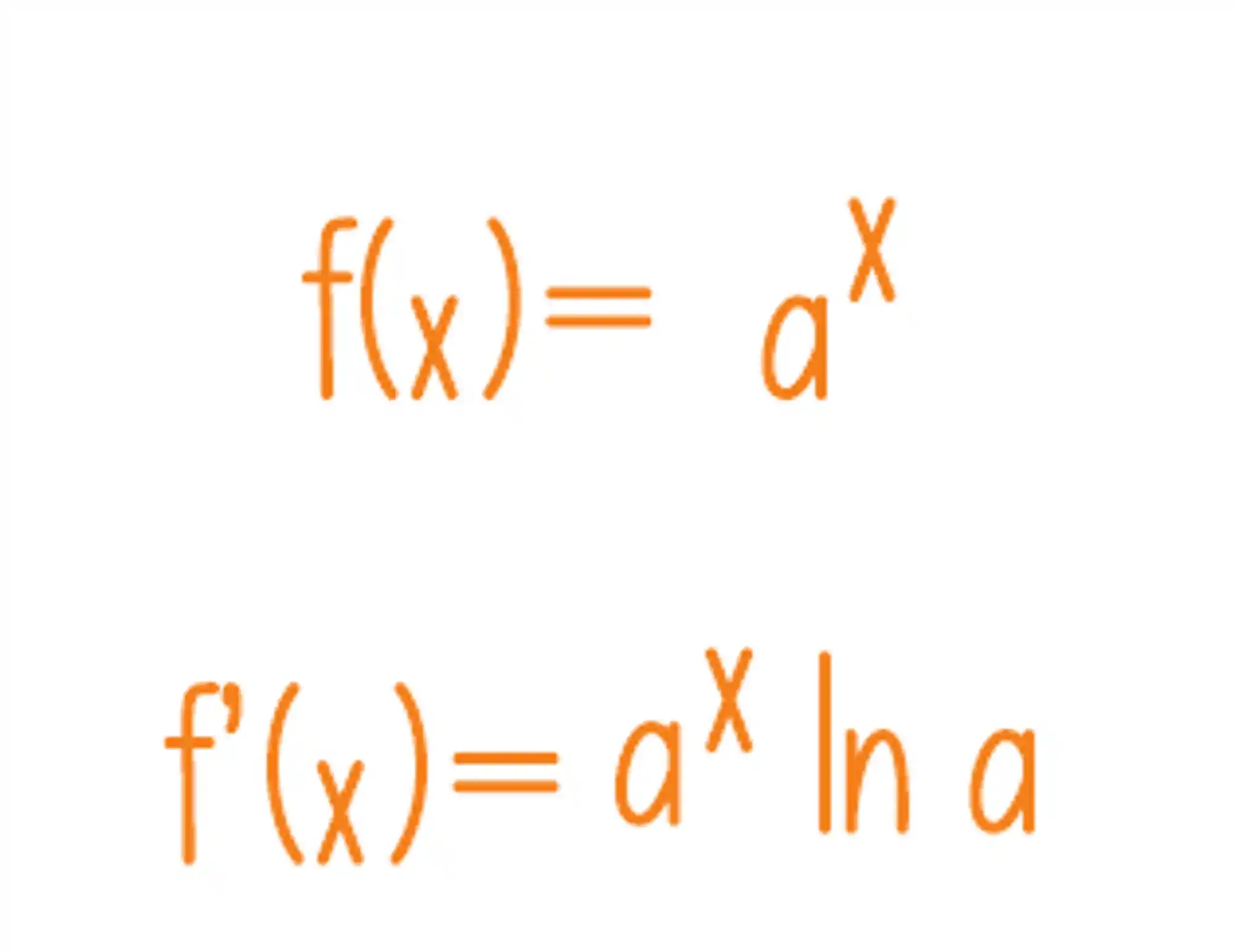
Derivada Exponencial
Derivada Exponencial

A função exponencial na base tem a propriedade de ser sua própria derivada. Ela é a derivada mais fácil que existe! 🤩

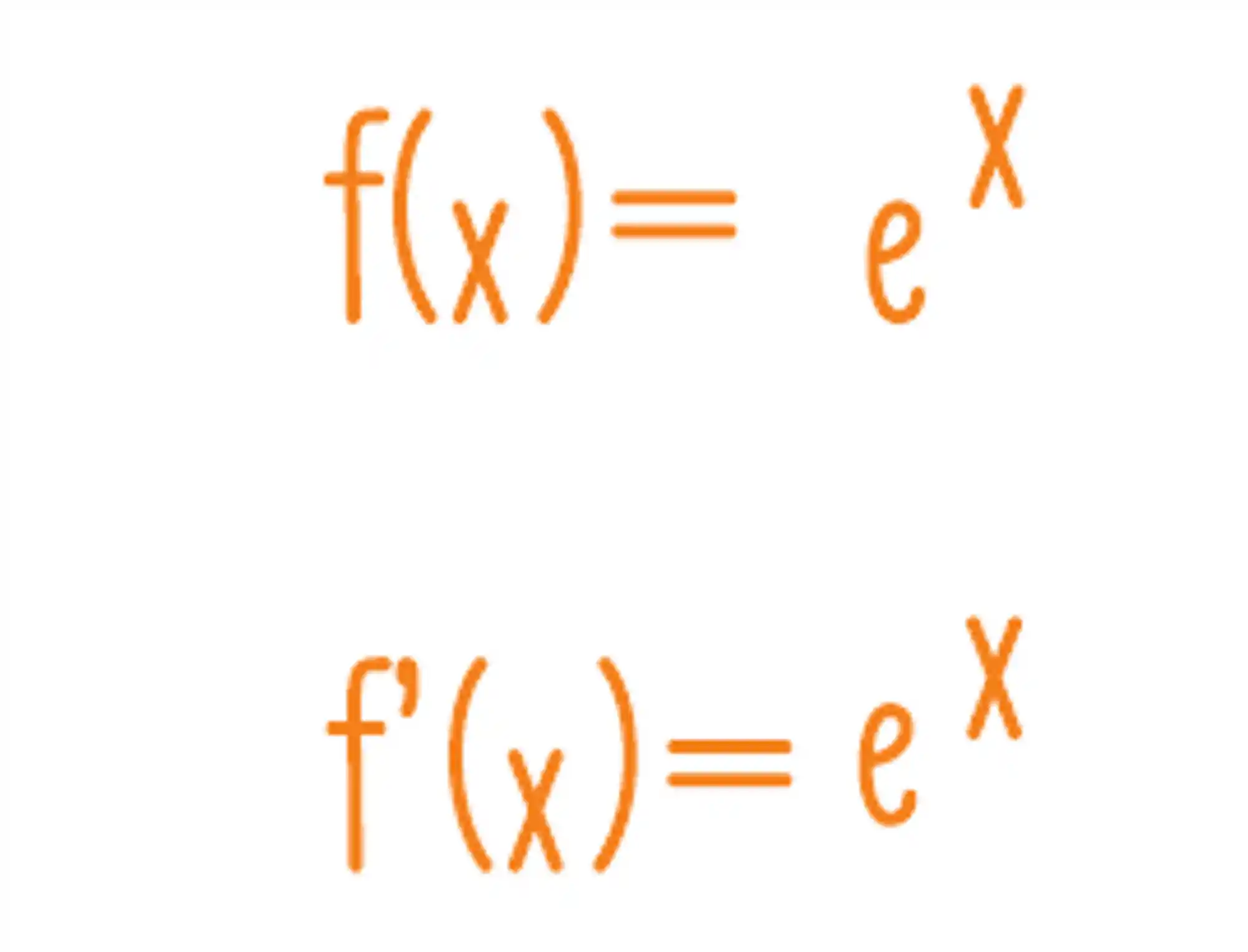
função exponencial na base e
função exponencial na base e

Mas é claro…sempre tem como complicar! Vou te mostrar um exemplo 👇

📢 Clique para ver mais:

Exemplo: Calcule a derivada de

Pra resolver esse problema vamos a fórmula da derivada exponencial e a regra da cadeia! Para isso precisamos reorganizar nossa função:

Para aplicar a regra da cadeia a gente precisa derivar e . Vamos começar com a derivada exponencial:

Sério…essa é a derivada mais fácil do mundo! Agora derivamos com respeito a :

Aplicando a regra da cadeia, temos:

Prontinho, temos a nossa derivada! Você também pode conferir esse conteúdo em vídeo:

Derivada Logarítmica

Para calcularmos a derivada de uma função logarítmica, usamos a seguinte fórmula:

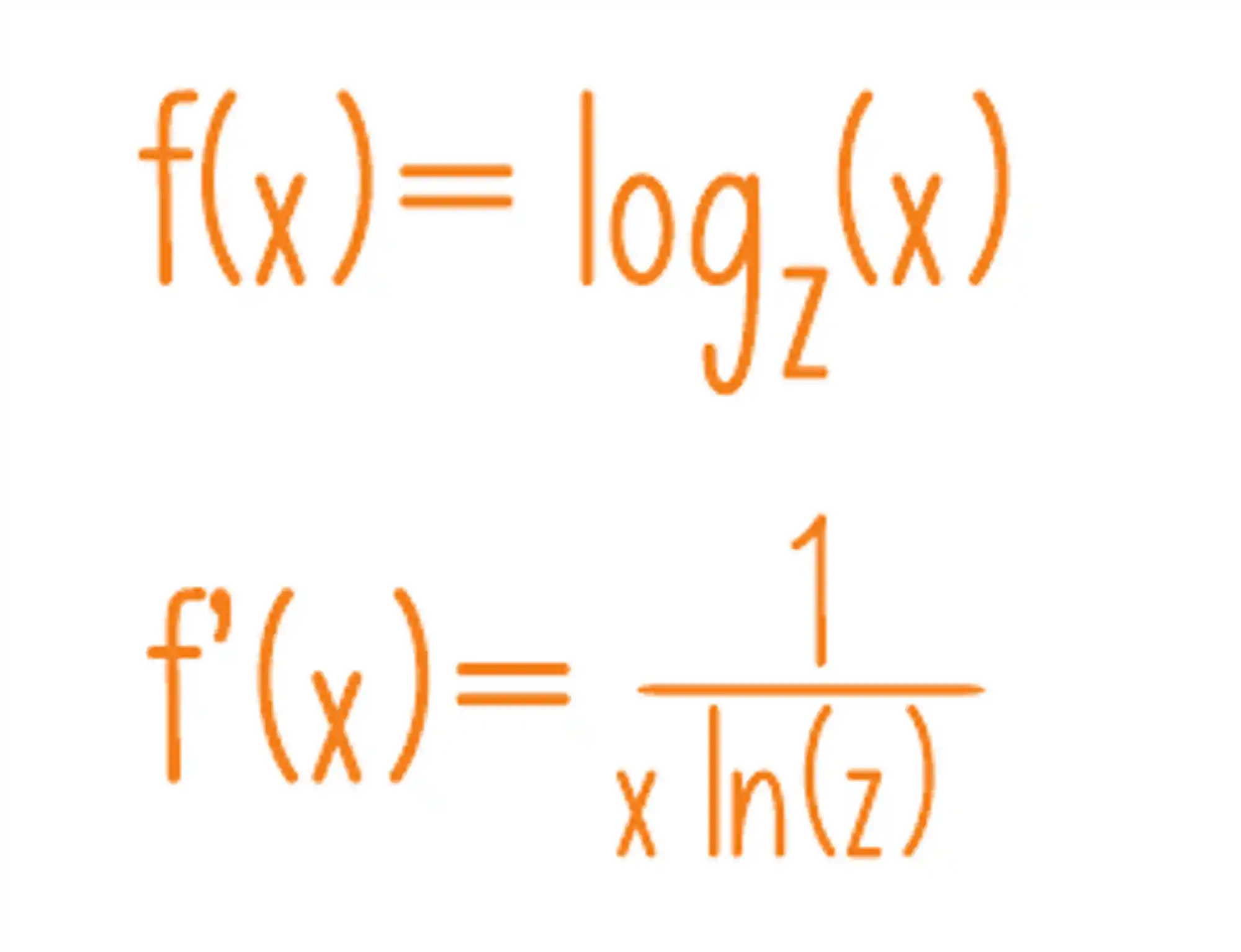
Derivada de log
Derivada de log

Essa fórmula acima serve para logaritmos de qualquer base, mas quando estamos falando do log neperiano temos uma fórmula ainda mais simples:

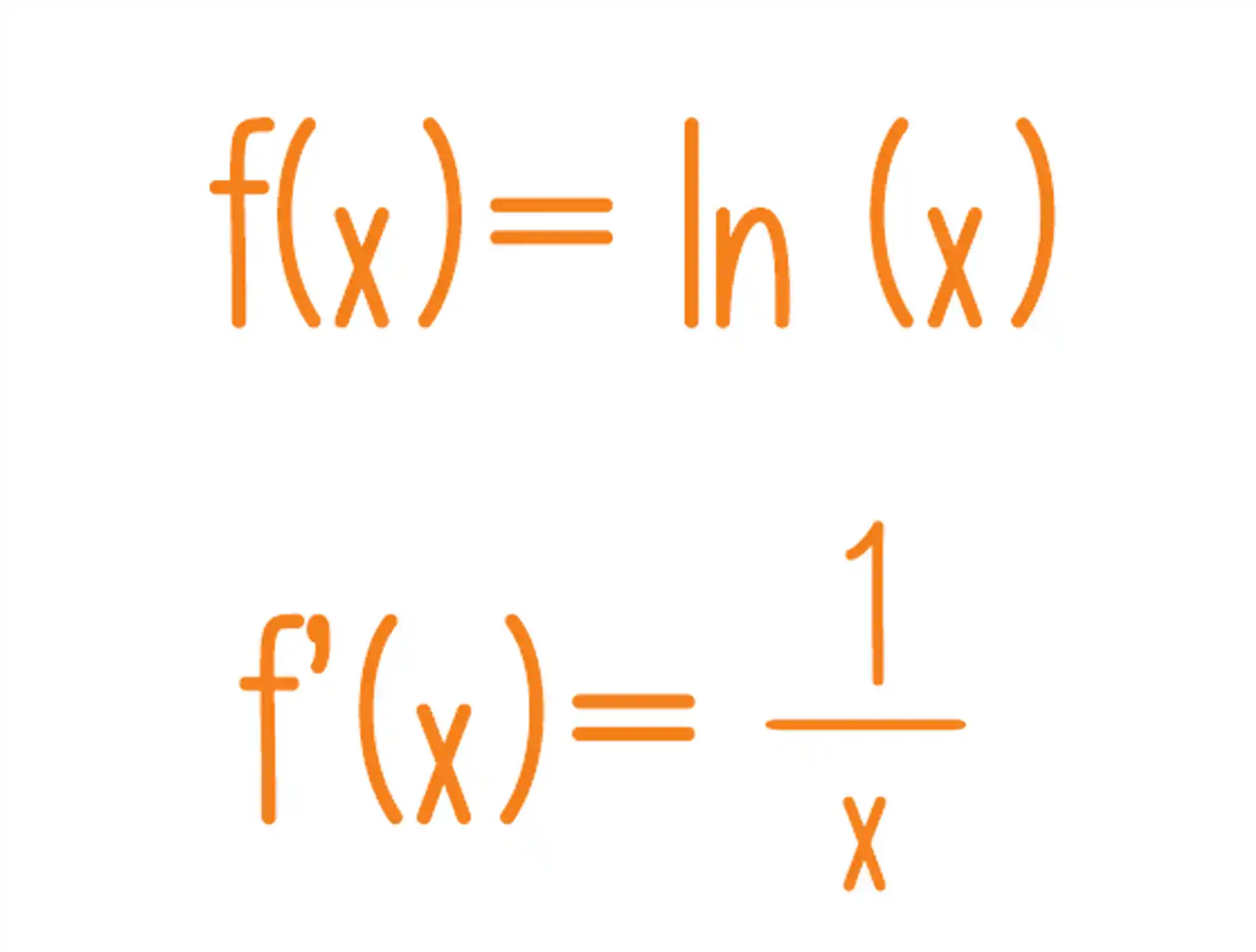
Derivada de logaritmo neperiano
Derivada de logaritmo neperiano

Na verdade a fórmula é a mesma, essa versão ai de cima só esta simplificada e eu vou te provar! Se liga:

Mas é igual a um, logo:

Tcharaãam!

Exemplo: Calcule a derivada de

Para resolver esse problema temos que usar a regra da cadeia! Para isso definimos :

Substituindo na nossa função:

Para derivar vamos usar a fórmula da derivada de log:

Derivamos em relação a :

Aplicamos a regra da cadeia:

Damos uma arrumada:

Temos a nossa derivada! Agora vamos praticar com mais exercícios?

Derivada Logarítmica

Exercícios Resolvidos

Exercício Resolvido #1

Elaboração própria

Calcule a derivada da função abaixo:

y = 10 x

Passo 1

Aplicando a regra da derivada de funções exponenciais:

f x = a x → f ' x = a x ln ⁡ a

Teremos:

y = 10 x

d y d x = 10 x ln ⁡ 10

Resposta

d y d x = 10 x ln ⁡ 10

Exercício Resolvido #2

Elaboração Própria

Seja a função

f x = k e x ,     k ∈ R

O que se pode dizer sobre a razão f ' x f x ?

Passo 1

Vamos achar a derivada da f .

A função nada mais é que a função exponencial e x multiplicada pela constante k . Então temos que:

d f d x = k d e x d x

Passo 2

Temos que:

f x = a x → f ' x = a x l n a  

Só que pra exponencial, a derivada acaba sendo ela mesma, pois l n e   = 1 :

d ( e x ) d x = e x l n e   = e x

Então vamos ter:

f ' x = k e x = f x

Passo 3

Ou seja

f ' x f x = k e x k e x = 1

Qualquer função da forma k e x com k constante é igual a sua derivada! Então pra qualquer k diferente de 0 essa razão dá 1 .

Resposta

P a r a   q u a l q u e r   k   d i f e r e n t e   d e   0   a   r a z ã o   v a l e   1 .

Exercício Resolvido #3

Elaboração própria

Calcule a derivada da função:

y = ln ⁡ 3 x

Passo 1

Aplicando a regra da derivada de logaritmos, teremos:

y = ln ⁡ 3 x

Antes de mais nada, vamos usar as propriedades de log para melhorar essa conta

y = ln ⁡ 3 x = ln ⁡ 3 + ln ⁡ x

Agora vamos derivar as partes

Passo 2

Temos

d y d x = ln ⁡ 3 ' + ln ⁡ x '

Lembrando que ln ⁡ 3 é uma constante, então

ln ⁡ 3 ' = 0

E

ln ⁡ x ' = 1 x

Assim, vamos ter:

d y d x = 0 + 1 x

d y d x = 1 x

Resposta

d y d x = 1 x

Exercício Resolvido #4

Elaboração própria

Calcule a derivada da função:

y = 5 e 3 x e 2 x + 3 ln ⁡ x

Passo 1

Temos uma soma para derivada, para isso vamos usar as propriedades das derivadas, para organizar vamos fazer:

y = y 1 + y 2

Com

y 1 = 5 e 3 x e 2 x

E

y 2 = 3 ln ⁡ x

Assim, vamos ter:

d y d x = d y 1 d x + d y 2 d x

Passo 2

Vamos começar derivando

y 1 = 5 e 3 x e 2 x

Aqui, como apareceram essas duas exponenciais com a mesma base e , o primeiro passo é arrumar esse cara, lembrando que uma divisão de exponenciais de mesma base dará uma exponencial com essa base e expoente valendo a diferença de seus expoentes:

y 1 = 5 e 3 x - 2 x

y 1 = 5 e x

Passo 3

Aplicando a regra da derivada de funções exponenciais:

f x = e x → f ' x = e x

Teremos:

y 1 = 5 e x

d y 1 d x = 5 e x ' = 5 e x

Passo 4

Agora, vamos derivar

ln ⁡ x

Usando as propriedades de derivadas, vamos ter:

y 2 = 3 ln ⁡ x

d y 2 d x = 3 ( ln ⁡ x ) '

d y 2 d x = 3 1 x

d y 2 d x = 3 x

Passo 5

Assim, vamos ter:

d y d x = d y 1 d x + d y 2 d x

Substituindo o que fizemos nos passos, vamos ter:

d y d x = 5 e x + 3 x

Resposta

d y d x = 5 e x + 3 x

Exercício Resolvido #5

George B. Thomas Jr., Cálculo volume I, 11ª ed. São Paulo: Pearson Education do Brasil Ltda, 2009, pp221 – 83

Determine a derivada de y em relação a x

y = log 5 ⁡ e x

Passo 1

Aqui teremos que aplicar uma propriedade importante dos logaritmos. Se temos um logaritmo com uma base qualquer e logaritmando também com uma base qualquer, podemos dizer que:

log a ⁡ b c = c log a ⁡ b

Dessa maneira, teríamos nesse caso:

log 5 ⁡ e x = x log 5 ⁡ e

Como log 5 ⁡ e é um número real

log 5 ⁡ e ≅ 0,62

temos aqui que derivar um polinômio! Essa questão tá aqui para te lembrar dessa propriedade mesmo, por que não precisamos da derivada do log ou da exponencial para ela não.

Passo 2

Derivando, teremos:

y ' = log 5 ⁡ e ⏟ c o n s t a n t e x ' = log 5 ⁡ e ⏟ c o n s t a n t e x '

= log 5 ⁡ e

Resposta

y ' = log 5 ⁡ e

Exercícios de Livros Relacionados

Calcule g^' (x) g (x) = ln x
Calcule g^' (x) g (x) = log_3 x
Calcule g^' (x) g (x) = log_pi x
Calcule f^' (x) .f (x) = pi^x
Calcule f^' (x) .f (x) = 2^x