Equação de Euler de Ordem Superior
Produzido por Carolina SabaTeoria
Fala aí! Bora aprender como resolver uma Equação de Euler de Ordem Superior!? Então sem enrolação, ela tem essa carinha aqui:
Equação de Euler de Ordem Superior
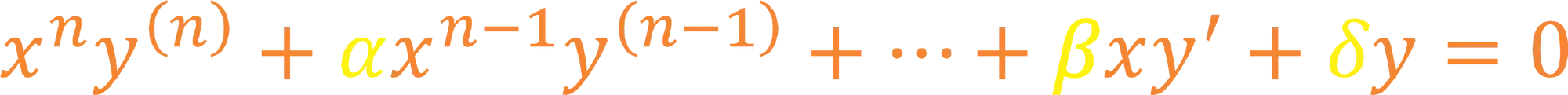
Onde
O modo de resolver Equações de Euler de Ordem Superior é bem parecido com o método de Euler-Cauchy aplicado a EDO’s de 2ª ordem! Se você não conhece esse método, eu sugiro dar um pulinho lá e conferir, é como se aquele fosse o nível 1 e aqui a gente já dá uma avançadinha. Sacou? 😉
Como Resolver uma Equação de Euler de Ordem Superior
A gente vai aprender na prática! Se liga só nesse exemplo:
Temos uma EDO de 3ª ordem com
Agora a gente coloca a mão na massa!
Passo 1: Calcular as Derivadas
Pra começar, a gente vai pegar a solução geral proposta e derivar ela três vezes! Ficamos então, com:
Passo 2: Substituir as Derivadas na EDO
Agora a gente pega as derivadas que terminamos de calcular e substituímos nessa EDO aqui:
Vamos ficar com:
Passo 3: Manipular a Equação
Colocando o
Opa! Temos o produto de duas parcelas dando zero. Isso significa que ou uma delas é zero, ou a outra. Ajeitando:
Ficamos com:
Pode ser escrito assim:
Colocando
Passo 4: Calcular as Raízes
Finalmente podemos calcular as raízes! Temos então:
Logo:
E:
Temos então as raízes complexas:
Prontinho, temos as raízes! Agora é só escrever
Passo 5: Escrever
Lá em cima a gente supôs a solução
Para as raízes complexas a gente vai usar esse quadrinho de soluções para o método de Euler:

A solução que estamos intensados é para
Multiplicidade de uma Raiz
A multiplicidade de uma raiz é a quantidade de vezes que essa raiz aparece. Quando temos uma equação de grau
Vamos ver um exemplo:
Essa é uma equação é de ordem
Substituindo:
Resolvendo essa equação vamos achar:
Voltando para
Repara que temos uma equação de grau 4, e achamos 4 raízes:
Você pode reparar que
Raízes com Multiplicidade 1
Nesse caso temos uma raiz aparecendo apenas uma vez. Então, temos que ficar atentos só se essa raiz é complexa ou não. Se a raiz não for complexa a solução é da forma:
E se tivermos uma raiz complexa ela vai ser da forma:
Quando temos uma raiz complexa dessa forma podemos garantir que vamos ter uma outra raiz complexa que vai ser:
E a solução dessas duas juntas será:
Raízes com Multiplicidade maior que 1
Imagina que temos uma EDO com uma raiz
Adicionamos o logaritmo de
Solução geral
Agora vamos entender como é a solução geral dessa EDO! Cada raiz tem uma solução associada
Para achar cada uma dessas soluções, basta a gente prestar atenção na multiplicidade de cada raiz, que o problema sai tranquilo!
Agora vamos exercitar!!!
Multiplicidade de uma Raiz
Exercícios Resolvidos
Exercício Resolvido #1
Denis G. Zill, Equações Diferenciais Volume I , 3ª ed. São Paulo: PEARSON Education do Brasil, 2007, pp. 284 - 19
Resolva a seguinte EDO:
Passo 1
Primeira coisa a ser feita é perceber que isso é uma equação de Euler. Então vamos supor a solução da forma:
Passo 2
Calculando as derivadas:
Passo 3
Substituindo na EDO temos:
Ajeitando:
Portanto, temos de resolver:
Passo 4
Como encontrar as raízes dessa equação??!
Vamos ver alguns candidatos a raízes dessa equação.
Qual o coeficiente do maior grau dessa equação? Neste caso vai ser , vamos chamar isso de
Qual o valor do cara sem a variável ? Vai ser , vamos chamar isso de
As possíveis raízes vão ser os divisores de sobre os divisores de , lembrando que para cada possibilidade vamos ter o cara podendo ser positivo ou negativo.
Nesse caso, os divisores de são: .Os divisores de são . Logo as possíveis raízes são:
Passo 5
Então temos que testar essas raízes na equação, como fazemos isso? É só substituir o valor na equação e ver se vai dar , se der o valor de é raiz, se não der ele não é raiz.
Testando cada um desses números, verificamos que são raízes. Tivemos sorte, porque apenas procurando entre esses valores já encontramos todas as raízes da equação. Caso encontrássemos apenas uma raiz, o próximo passo seria utilizar o método de briot-ruffini para encontrar as outras raízes.
Enfim temos as raízes:
Passo 6
Como as raízes são distintas a solução fica:
Resposta
Exercício Resolvido #2
Denis G. Zill, Equações Diferenciais Volume I , 3ª ed. São Paulo: PEARSON Education do Brasil ltda., 2007, pp. 284 - 22
Resolva a seguinte EDO:
Passo 1
Primeira coisa a ser feita é perceber que isso é uma equação de Euler. Então vamos supor a solução da forma:
Passo 2
Calculando as derivadas:
Passo 3
Substituindo na EDO temos:
Ajeitando:
Fazendo as contas vai ficar:
Temos de resolver:
Passo 4
Perceba que essa equação é o mesmo que:
Portanto as raízes são:
Passo 5
As raízes são complexas, então vamos pergar o primeiro conjugado delas, ou seja e :
A solução referente a e seria:
Porém essa solução já existe, então temos que multiplicá-la por
Fica assim:
Passo 6
Logo a solução geral da EDO será: