Equação de Euler-Cauchy
Produzido por Carolina SabaTeoria
A Equação de Euler-Cauchy, também conhecida como Equação de Cauchy-Euler é bem parecida com uma EDO de segundo ordem homogênea, mas tem uma diferença muito importante, os coeficientes não são números!!
Presta muita atenção na diferença entre elas, pra não ter confusão:
Equação de Euler-Cauchy e EDO de 2ª ordem
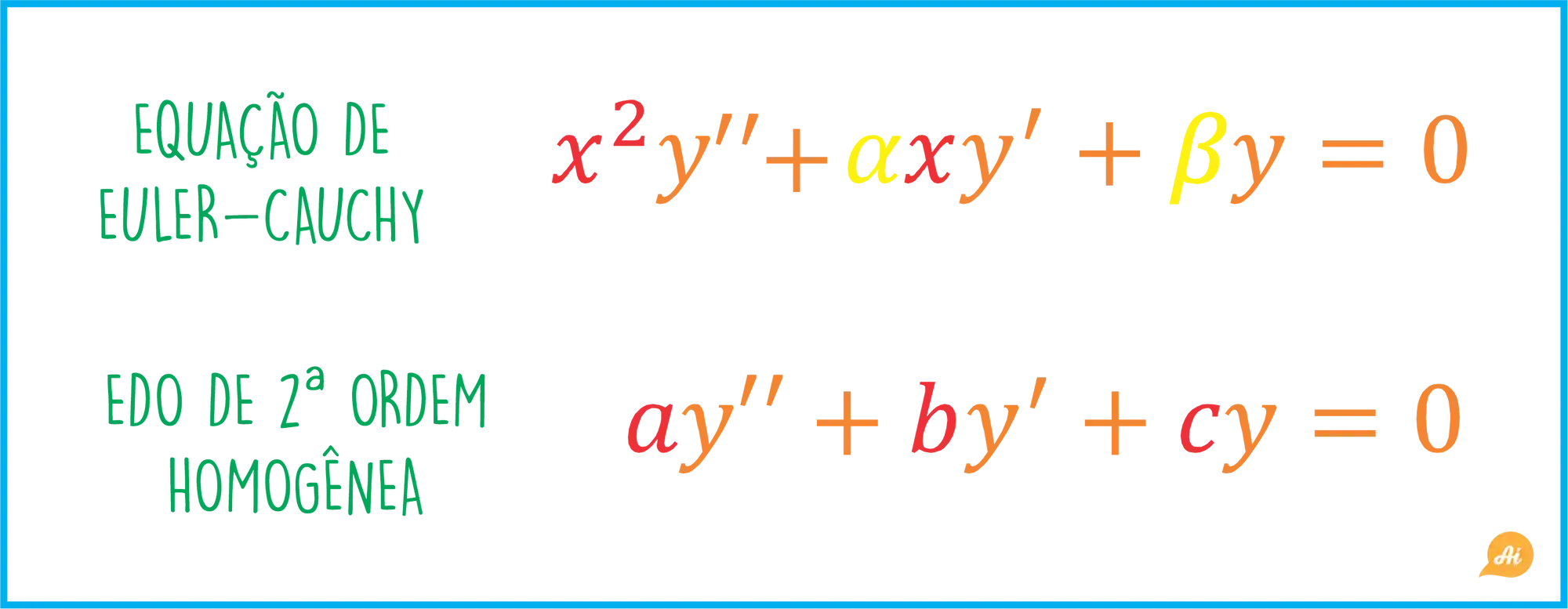
Percebeu a diferença?! Tanto na Equação de Euler-Cauchy, quanto na EDO de 2ª ordem homogênea temos o
Na EDO de 2º ordem homogênea temos apenas os coeficientes
já na na Equação de Euler-Cauchy temos o
E agora…como a gente faz pra lidar com esse
Calma que a gente vai aprender passo a passo do Método de Euler! 🤩
📢Clique para ver mais:
Método de Euler: Passo a Passo
Bora aprender na prática como resolver uma equação de Euler-Couchy?! Bora fazer um exemplo então, vamos encontrar a solução geral desse carinha aqui:
Já ficou atento no formatinho dela, né?
Passo 1: Colocar a EDO na Forma
Pro método de Euler funcionar, a nossa EDO precisa estar nesse formatinho ali de cima! Repara que o coeficiente de
Ela tá no formatinho certo, então não precisamos fazer nada aqui! Mas imagina que tivéssemos esse caso:
A gente poderia dividir toda a Equação por
Prontinho! Sem grandes problemas! Se você preferir você pode acompanhar o restante dessa resolução nesse vídeo iradoso aqui em baixo! 😉
Passo 2: Definir
Aqui também não tem mistério, é só a gente olhar pra a equação e pegar os coeficientes da segunda e da terceira parcelas. No nosso caso temos:
Passo 3: Escrever o Polinômio Característico
Quando temos uma Equação de Euler, caímos no seguinte polinômio característico:
Substituindo o
Mas da onde surgiu esse
Pra ficar mais claro vamos dar um passo pra trás e voltar na nossa equação e sugerir a solução
Derivando, ficamos com:
Arrumando, chegamos em:
Opaaa, chegamos no polinômio característico!!
Passo 3: Encontrar as Raízes do Polinômio Característico
Reparou que o polinômio característico é uma equação do segundo grau? Então resolvemos ela usando Bhaskara:
Onde:
Para o nosso exemplo, temos:
Resolvendo, achamos:
Passo 4: Escrever a Solução da EDO
Show! Agora partimos para a solução, que vai ser a combinação dessas respostas:
Resumindo, vimos que, quando estamos resolvendo uma equação pelo método de Euler, chegamos em um polinômio característico. Nesse ponto a gente precisa encontrar a solução do polinômio pra aí sim, encontrar o resultado final! Como caímos em uma equação do segundo grau, lá no polinômio característico, temos 3 possibilidades.
Vamos ver fazer o Método de Euler em cada uma delas.
Caso 1: Raízes Reais Distintas
Quando o
Esse foi justamente o nosso caso, lembra?
Caso 2: Raízes Reais Iguais
Agora, quando o
Percebe que tem um
Caso 3: Raízes Complexas
E pra encerrar, quando o
Nesse quadro resumo a gente tem todas as informações que você precisa, sobre o Método de Euler, organizadas:

Agora vamos praticar com exercícios!?
Caso 1: Raízes Reais Distintas
Caso 2: Raízes Reais Iguais
Caso 3: Raízes Complexas
Exercícios Resolvidos
Exercício Resolvido #1
William E. Boyce e Richard C. DiPrima, Equações diferenciais elementares e problemas de contorno, 9ª ed., Rio de Janeiro: LTC, 2010, pp. 216, exercício 9
Determine a solução geral da equação diferencial dada.
Passo 1
Olhando para a EDO, vemos que é uma Equação de Euler de coeficientes
Se procurarmos soluções do tipo , temos então a seguinte equação característica:
Passo 2
Como , temos uma raiz dupla , as soluções da EDO são, então:
Resposta
Exercício Resolvido #2
Solução de EDO – Ponto singular – equação de Euler
Considere a seguinte família de equações de Euler:
Onde é uma constante real.
- Encontre a solução da equação homogênea correspondente a que satisfaz as seguintes condições:
- Seja uma solução qualquer de com . Calcule o valor de .
onde é a base do logaritmo neperiano.
Sugestão: encontre uma equação de Euler que seja satisfeita pela função .
Passo 1
Letra a)
Temos o seguinte:
Precisamos deixar sozinho, então
Olhando para a EDO, vemos que é uma Equação de Euler de coeficientes
Se procurarmos soluções do tipo , temos então a seguinte equação característica:
Resolvendo essa equação
Passo 2
Como , temos uma raiz dupla , as soluções da EDO são, então:
Substituindo o valor de :
Passo 3
Usando as condições
Temos
Passo 4
Substituindo na expressão de :
Passo 5
Letra b)
Com , a equação passa a ser
Fazendo
Temos
E a solução dessa EDO nós já temos do item anterior:
Fazendo, então, :
Passo 6
Vamos calcular o limite disso aí entao
Aplicando L’Hopital
Resposta
Exercício Resolvido #3
William E. Boyce e Richard C. DiPrima, Equações diferenciais elementares e problemas de contorno, 9ª ed., Rio de Janeiro: LTC, 2010, pp. 216, exercício 36
Encontre todos os valores de para os quais todas as soluções de tendem a zero quando .
Passo 1
Olhando para a EDO, vemos que é uma Equação de Euler de coeficiente ( é o que queremos encontrar).
Se procurarmos soluções do tipo , temos então a seguinte equação característica:
Como nós não conhecemos , não sabemos se , ou , então, vamos ter que analisar a questão para cada um desses três casos.
Passo 2
Supondo que
- Encontrar o intervalo de
- Encontrar a solução geral de
- Encontrar que faz
Então, estamos analisando esses valores de , que fazem ser positivo.
Nesse caso, temos duas raízes reais distintas:
E as soluções da EDO são do tipo
O problema pede que as soluções tendam a zero quando , não é? Em outras palavras, queremos:
Isso ocorre quando for elevado a um número positivo, ou seja, quando e .
Caso contrário, se for elevado a uma raiz negativa, como por exemplo, temos . Quando , isso tende a infinito. Se a raiz for nula, temos e a solução continua sem tender para zero.
Portanto, precisamos de raízes positivas:
Para não complicar muito as coisas, já vamos considerar valores de positivos, que é o caso 1. Sendo assim, a primeira inequação é satisfeita para qualquer positivo, portanto, para . Falta, então, analisar a segunda.
Da mesma forma que na primeira, temos que ter , portanto, , esse é o valor máximo que assume. Mas essa inequação não é satisfeita para qualquer , veja que, para termos positiva precisamos de:
Se essa raiz for maior que , teremos , a raiz fica negativa. Certo? Então, a solução da segunda inequação é .
Como nós precisamos que E sejam positivas temos que fazer a interseção entre as soluções das duas inequações, que é
Passo 3
Supondo que
- Encontrar o intervalo de
- Encontrar a solução geral de
- Encontrar que faz
- Fazer a interseção entre os itens 1 e 3
Então, agora estamos analisando apenas esses valores de , que fazem ser igual a zero.
Nesse caso, encontramos a raiz dupla da equação característica:
As soluções da Equação de Euler são do tipo:
O problema pede que as soluções tendam a zero quando , ou seja:
Novamente, isso deve ocorrer quando for elevado a um número positivo, ou seja, quando , pelo mesmo motivo que vimos no caso anterior. Veja que aparece um limite do tipo . Como a gente sabe que , a gente tem que dar uma olhada com mais calma nesse limite que apareceu, pra ver se ele realmente vai pra zero.
Supondo que
Caímos numa indeterminação do tipo . Usando nosso velho amigo L’Hospital:
O limite vai pra zero! Queremos, então:
Isso é sempre verdade, logo, sempre que for zero, o problema é satisfeito.
Para o caso 2, temos então a seguinte solução:
Passo 4
Supondo que
- Encontrar o intervalo de
- Encontrar a solução geral de
- Encontrar que faz
- Fazer a interseção entre os itens 1 e 3
Nessa região temos negativo, o que nos leva a duas raízes complexas para a equação característica:
Veja que, para colocar em evidência, tivemos que mudar o sinal do que está dentro da raiz!
As soluções da Equação de Euler são do tipo:
Já sabemos que .
O problema pede que as soluções tendam a zero quando , ou seja:
Bom, esse limite já dá zero, não é? Temos:
Para qualquer valor de (e, portanto, de ).
Estamos analisando o caso em que , não é? Então, nosso problema é satisfeito no caso 3 para:
Passo 5
A resposta do problema é a junção de todas as soluções que encontramos para os três casos de valores de , ou seja:
A soma disso tudo dá