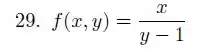Exercícios de Curvas de Nível - Lista de Exercícios Resolvida

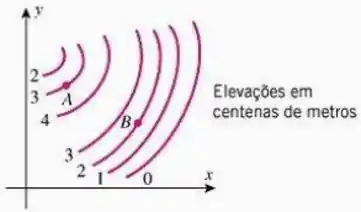
Em cada parte, as questões se referem ao mapa de contorno na figura abaixo.

a) O ponto ou é o ponto mais alto? Explique seu raciocínio.

b) O ponto ou está na inclinação mais íngreme? Explique seu raciocínio.

c) Iniciando em e movendo-se de tal modo que permanece constante e cresce, a elevação começará a crescer ou decrescer?

d) Iniciando em e movendo-se de tal modo que permanece constante e cresce, a elevação começará a crescer ou decrescer?

e) Iniciando em e movendo-se de tal modo que permanece constante e decresce, a elevação começará a crescer ou decrescer?

f) Iniciando em e movendo-se de tal modo que permanece constante e decresce, a elevação começará a crescer ou decrescer?

Desenhe as curvas de nível e determine a imagem:

Considere a função

1. Escreva a equação da curva de nível de que contém o ponto e da curva de nível que contém o ponto
2. Mais geralmente, escreva a equação da curva de nível de que contém o ponto , com .
3. Mostre que o valor de sobre a reta é constante, isto é, que está contida em um conjunto de nível de .
4. Mostre que o valor de sobre a reta é constante, isto é, que está contida em um conjunto de nível de .
5. Se, por um momento, representasse um lucro e você fosse um empresário, em qual reta você gostaria de estar: ou ? Justifique sua resposta.

A temperatura em um ponto de uma placa de metal plana é graus.

1. Encontre a temperatura no ponto .
2. Encontre a equação da curva ao longo da qual a temperatura tem um valor constante e igual a graus.
3. Esboce a curva do item (b).

Seja

a) Esboce a curva de nível de que corresponde ao nível . Em que pontos essa curva intercepta o eixo ?

Faça o mapa de contorno da função mostrando várias curvas de nível.

2) considere a função .

a) Esboce, no plano cartesiano abaixo, o domínio de , indicando pontos que não pertençam ao seu domínio com linhas tracejadas. Determine as curvas de nível e de e esboce suas imagens, também no plano abaixo.

b) Decida, justificando, se existe.

Suponha que representa o valor da temperatura em sobre os pontos do plano .

1. Desenhe a isoterma correspondente a

Considere . Determine o domínio de e esboce as curvas de níveis , e

Seja .

a) Esboce uma família de curvas de nível de .

b) Encontre a interseção do gráfico de com o plano e descreva a interseção do gráfico de com cada plano , em que .

c) Descreva e esboce o gráfico de .

d) Encontre uma parametrização para a interseção do gráfico de com o plano , explicitando o domínio.

Seja

a) Encontre e esboce o domínio de .

b) Esboce a curva de nível de que corresponde ao nível . Em que pontos essa curva intercepta o eixo ?

c) Encontre uma parametrização para a curva do item

d) Sabendo que a imagem da curva , , está contida no gráfico de , encontre a função e dê a equação da reta tangente a em .

Seja . Determine a equação da reta tangente à curva de nível no ponto .

Seja

1. Num mesmo sistema de coordenadas, esboce as curvas de nível de f nos níveis e

1) Seja . Classifique e esboce as curvas de nível . Para quais valores de temos que a curva de nível correspondente é não vazia? Esboce o gráfico de .

Nos seguintes exercícios, encontre o domínio , encontre a imagem , e descreva as curvas de nível da função:

a)

Seja a função, definida em

Dada por

Determine equações para as curvas de nível de quando . Faça um esboço delas (em linha cheia) e da restrição no domínio (em pontilhado).

Dada a função .

Determine e identifique as curvas de nível de .

Resolva o que se pede:

b) Esboçe as curvas de nível da função

Esboce a curva de nível da função que passa no ponto .Observe que o comportamento da função ao longo da tangente que passa no ponto

Considere a curva

A imagem de está contida na curva de nível:

1. da função
2. da função
3. da função
4. da função

Determine a equação da reta tangente ao gráfico da função dada passando pelo ponto , caso elas existam.

(b) e

Considere a função

Então

a) a curva de nível de está contida em uma parábola.

b) a curva de nível de é uma elipse.

c) a curva de nível de é uma hipérbole.

d) a curva de nível de está contida em uma elipse.

e) a curva de nível de é um conjunto vazio.

8- Seja .

b) Identifique as interseções do gráfico de com os planos , , , e .

Seja

a) Determine e esboce a curva de nível de que passe pelo ponto (1,1).

b) Determine e esboce a curva de nível de que passe pelo ponto (1,1).

c) A afirmação “As curvas de nível de e dos itens anteriores são ortogonais no ponto (1,1)” é verdadeira ou falsa? Justifique sua resposta.

Considere a função

1. Escreva a equação da curva de nível de que contém o ponto e da curva de nível que contém o ponto
2. Mais geralmente, escreva a equação da curva de nível de que contém o ponto , com .
3. Mostre que o valor de sobre a reta é constante, isto é, que está contida em um conjunto de nível de .
4. Mostre que o valor de sobre a reta é constante, isto é, que está contida em um conjunto de nível de .
5. Se, por um momento, representasse um lucro e você fosse um empresário, em qual reta você gostaria de estar: ou ? Justifique sua resposta.

2. Considere a função .

b) Esboce a curva de nível de que passa pelo ponto .

Seja . Determine equações para as curvas de nível de para e . Faça o esboço dessas curvas.

1.2. Esboce uma família de curvas de nível das seguintes funções:

b)

1.2. Esboce uma família de curvas de nível das seguintes funções:

c)

1.7. Seja .

a. Esboce as curvas de nível de dos níveis , e

1.7. Seja .

b. Encontre uma curva derivável , definida num intervalo , cuja imagem seja a curva de nível de do nível .

1.2. Esboce uma família de curvas de nível das seguintes funções:

a)

Seja a temperatura numa chapa de aço plana. Dado o ponto determine:

1. O conjunto de pontos onde a temperatura é igual a

Quais são as curvas de nível da função do item (1). Faça um esboço da curva de nível 6

2) Representar no plano cartesiano as curvas de nível das funções abaixo correspondentes aos valores de nível dados

(b) , , , , .

2) Representar no plano cartesiano as curvas de nível das funções abaixo correspondentes aos valores de nível dados

(c) , , , , .

2) Representar no plano cartesiano as curvas de nível das funções abaixo correspondentes aos valores de nível dados

(d) , , , .

2) Representar no plano cartesiano as curvas de nível das funções abaixo correspondentes aos valores de nível dados

(f) , , e .

2) Representar no plano cartesiano as curvas de nível das funções abaixo correspondentes aos valores de nível dados

(e) , , e .

6) Esboce o gráfico das funções abaixo (onde ):

(a)

6) Esboce o gráfico das funções abaixo (onde ):

(b)

6) Esboce o gráfico das funções abaixo (onde ):

(e)

6) Esboce o gráfico das funções abaixo (onde ):

(g)

6) Esboce o gráfico das funções abaixo (onde ):

(c)

6) Esboce o gráfico das funções abaixo (onde ):

(f)

6) Esboce o gráfico das funções abaixo (onde ):

(h)

1.6. Considere a curva , . A imagem de está contida na curva de nível

a. da função ;

b. da função ;

c. da função ;

d. da função ;

e. da função .

Resolva o que se pede:

Faça o mapa de contorno da função abaixo, mostrando várias curvas de nível:

Dada a função .

Determine algebricamente e identifique as curvas de nível de .

Considere a função

Então

a) a curva de nível de está contida em uma hipérbole.

b) a curva de nível de é uma elipse.

c) a curva de nível de é uma parábola.

d) a curva de nível de está contida em uma elipse.

e) a curva de nível de é um conjunto vazio.

Determine o domínio da função dada e represente-o graficamente. Esboce duas curvas de nível para cada função.

Determine o domínio da função dada e represente-o graficamente. Esboce duas curvas de nível para cada função.

Determine o domínio da função dada e represente-o graficamente. Esboce duas curvas de nível para cada função.

Determine o domínio da função dada e represente-o graficamente. Esboce duas curvas de nível para cada função.

Determine o domínio da função dada e represente-o graficamente. Esboce duas curvas de nível para cada função.

Determine o domínio da função dada e represente-o graficamente. Esboce duas curvas de nível para cada função.

3 - Considere a função e a região .

(a) Esboce em um único desenho a região e as curvas de nível de .

1.6) Faça os mapas de contornos das funções a seguir, mostrando várias curvas de nível.

a)

b)

c)

d)

1.6) Faça os mapas de contornos das funções a seguir, mostrando várias curvas de nível.

a)

b)

c)

d)

1.6) Faça os mapas de contornos das funções a seguir, mostrando várias curvas de nível.

a)

b)

c)

d)

8. Esboce os gráficos das funções abaixo. Reconheça todos os gráficos, exceto um, como superfícies dadas por (ou contidas em) quadráticas, identificando-as:

(a)

Seja uma função cujo valor do ponto representa a temperatura em neste ponto. Se é dada por:

1. Determine e esboce graficamente o domínio da função
2. Esboce a isoterma de temperatura
3. Encontre o(s) ponto(s) onde a temperatura seja máxima ao longo da reta

(1) Seja .

b) Descreva as curvas de nível de , esboçando na sua figura do domínio curvas típicas

Considere a função .

b) Desenhe as curvas de nível de , para os níveis , e .

Considere a função .

b) Obtenha as curvas de nível . Quais são os valores de permitidos? Por quê?

Considere a função

Então

a) a curva de nível de está contida em uma elipse.

b) a curva de nível de é uma hipérbole.

c) a curva de nível de está contida em uma elipse.

d) a curva de nível de é uma parábola.

e) a curva de nível de é um conjunto vazio.

1.6) Faça os mapas de contornos das funções a seguir, mostrando várias curvas de nível.

a)

b)

c)

d)

Dada

c) Esboce o e a curva de nível .

8. Esboce os gráficos das funções abaixo. Reconheça todos os gráficos, exceto um, como superfícies dadas por (ou contidas em) quadráticas, identificando-as:

(b)

8. Esboce os gráficos das funções abaixo. Reconheça todos os gráficos, exceto um, como superfícies dadas por (ou contidas em) quadráticas, identificando-as:

(e)

8. Esboce os gráficos das funções abaixo. Reconheça todos os gráficos, exceto um, como superfícies dadas por (ou contidas em) quadráticas, identificando-as:

(f)

8. Esboce os gráficos das funções abaixo. Reconheça todos os gráficos, exceto um, como superfícies dadas por (ou contidas em) quadráticas, identificando-as:

(h)

9. Em cada item, esboce no mesmo plano coordenado as curvas de nível para :

(a)

8. Esboce os gráficos das funções abaixo. Reconheça todos os gráficos, exceto um, como superfícies dadas por (ou contidas em) quadráticas, identificando-as:

(g)

9. Em cada item, esboce no mesmo plano coordenado as curvas de nível para :

(b)

22. Descreva e esboce as curvas de nível e o gráfico da função:

a)

22. Descreva e esboce as curvas de nível e o gráfico da função:

b)

22. Descreva e esboce as curvas de nível e o gráfico da função:

c)

Descreva e esboce as curvas de nível e o gráfico da função:

22. Descreva e esboce as curvas de nível e o gráfico da função:

e)

Descreva e esboce as curvas de nível e o gráfico da função:

Descreva e esboce as curvas de nível e o gráfico da função:

9. Em cada item, esboce no mesmo plano coordenado as curvas de nível para :

(f)

22. Descreva e esboce as curvas de nível e o gráfico da função:

d)

Descreva e esboce as curvas de nível e o gráfico da função:

9. Em cada item, esboce no mesmo plano coordenado as curvas de nível para :

(d)

2) Representar no plano cartesiano as curvas de nível das funções abaixo correspondentes aos valores de nível dados

(a) , , , , .

10. Descreva a superfície de nível para :

(a)

11. Ache a equação do conjunto de nível de que passe pelo ponto dado:

(b) ,

11. Ache a equação do conjunto de nível de que passe pelo ponto dado:

(c) ,

12. (a) Encontre alguma função (especificando seu domínio, contradomínio e sua lei), que tenha a reta de equação como uma curva de nível.

6) Esboce o gráfico das funções abaixo (onde ):

(d)

13. Se dá a temperatura num ponto sobre uma placa delgada de metal no plano-, , então as curvas de nível de são chamadas de curvas isotérmicas (todos os pontos sobre cada uma dessas curvas possuem a mesma temperatura). Suponha que uma placa ocupe o primeiro quadrante e .