Curvas de nível e esboço de gráfico
Produzido por Bruno NeresTeoria
E aí, você chegou no Responde Aí! Aqui você vai encontrar tudo o que precisa sobre Curvas de nível e esboço de gráfico em funções de duas variáveis.
Então, dá uma olhada nessa aula maneira:
Show! Quer saber mais? É só continuar lendo!
Curvas de nível a partir de um gráfico
As curvas de nível são uma projeção de um gráfico 3D em um plano 2D. Dá uma olhada nesse exemplo.
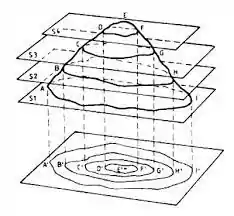
Em cima a gente tem um gráfico em 3D. Nesse gráfico, a gente faz vários cortes em alturas diferentes, e desenhamos o contorno desses cortes no plano 2D. As curvas de nível são os contornos de diferentes alturas de uma superfície 3D./
Esboço de gráfico a partir das curvas de nível.
Beleza, mas e se a gente quiser o inverso: criar um gráfico 3D partindo das curvas de nível 2D?
Passo 1: Imagine que temos o seguinte mapa de contorno:
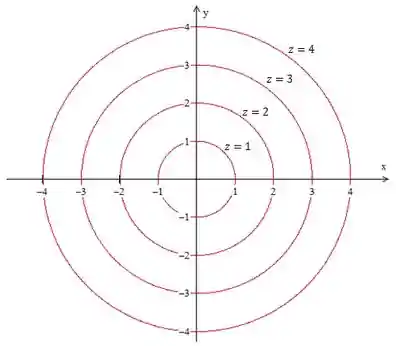
Passo 2: Repara que ao longo de cada curva de nível a gente possui o valor
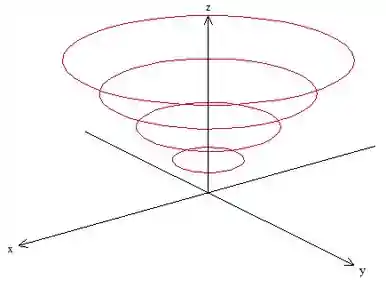
Agora temos um esboço geral do gráfico.
Passo 3: Pra terminar o gráfico, a gente utiliza o esboço e “ligar os pontos”, para gerar uma malha tridimensional
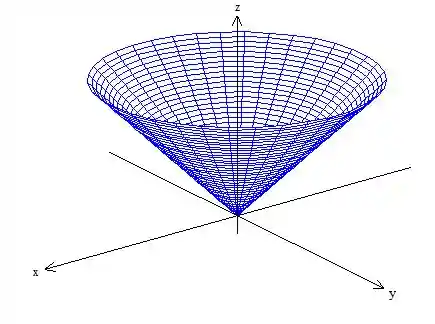
Viu como é tranquilo? Então dá uma olhada aqui e em baixo e confere alguns exercícios 👇