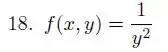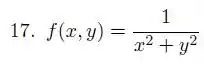Exercícios de Funções de 2 variáveis, Curvas de Nível e Gráfico - Lista de Exercícios Resolvida
Questão 1
Um mapa de contorno de uma função é mostrado. Use-o para fazer um esboço do gráfico da .
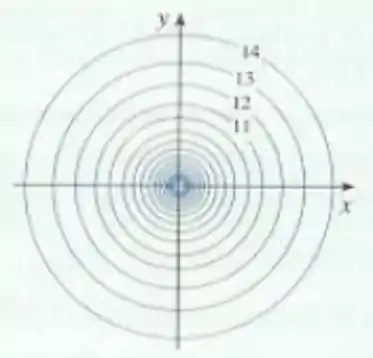
Questão 2
Faça o esboço do mapa de contorno e do gráfico da função e compare-os.
Ver solução completaQuestão 3
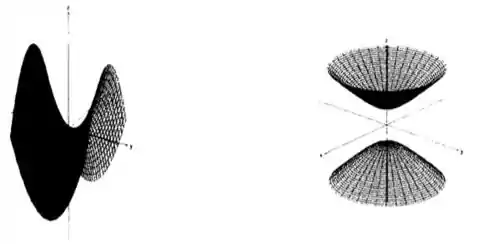
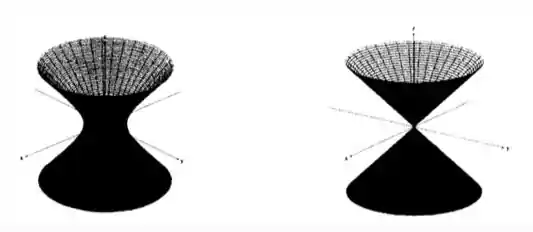
Cada uma das figuras abaixo representa uma superfície. Na coluna da tabela, temos uma equação para cada uma dessas superfícies. Cada superfície contém a imagem de uma das curvas da coluna . Escreva abaixo de cada figura qual é a curva cuja imagem está contida na superfície que ela representa:

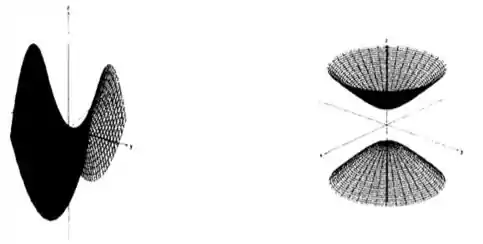
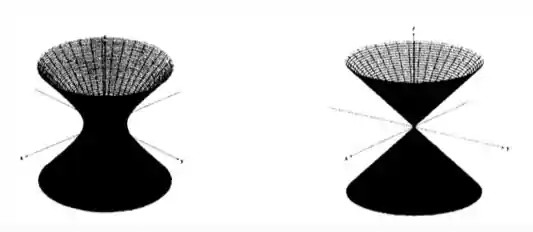
Questão 4
Em cada parte, associe o mapa de contorno com uma das funções
por inspeção, e explique seu raciocínio. Quanto maior o valor de , mais clara fica a cor no mapa de contorno e os contornos correspondem a valores igualmente espaçados de .
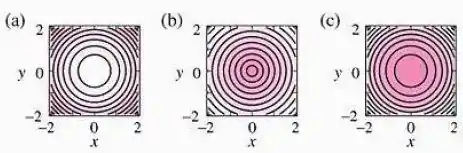
Questão 5
Na figura estão representadas curvas de nível da função . Escreva uma expressão adequada para .
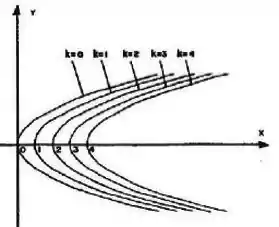
Questão 6
Os mapas de contorno abaixo (figuras , e ) correspondem a que gráficos (figura , , ou )?
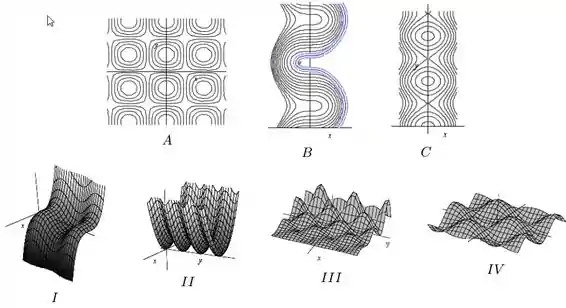
- , ,
- , ,
- , ,
- , ,
- , ,
- , ,
Questão 7
Considere . Determine:
- O domínio de ;
- As curvas de nível e o gráfico de ;
Questão 8
Considere a função
a) Esboce o gráfico de .
b) Identifique a curva de nível que contém o ponto .
Ver solução completaQuestão 9
Considere a função
a) Encontre o domínio e a imagem de .
b) O gráfico de é uma superfície quádrica? Se a resposta for sim, identifique a superfície e esboce o gráfico de .
c) Identifique as curvas de nível da função e esboce um mapa de contorno. Explique a relação entre o mapa de contorno e o gráfico de
Ver solução completaQuestão 11
Nos seguintes exercícios, encontre o domínio , encontre a imagem , e descreva as curvas de nível da função:
f)
Ver solução completaQuestão 12
Nos seguintes exercícios, encontre o domínio , encontre a imagem , e descreva as curvas de nível da função:
b)
Ver solução completaQuestão 13
Nos seguintes exercícios, encontre o domínio , encontre a imagem , e descreva as curvas de nível da função:
d)
Ver solução completaQuestão 15
Considere as funções:
b) . Para quais valores de e temos ? Represente graficamente a resposta.
Ver solução completaQuestão 16
9 - Associe a função com seu gráfico (indicado por na Figura 1) e com suas respectivas curvas de nível (indicado por na Figura 2).

a)
b)
c)
d)
e)
f)
Ver solução completaQuestão 17
Na figura temos, respectivamente, o desenho das curvas de nível das seis funções a seguir.
Faça a associação destas seis curvas de nível com cada um dos seis gráficos apresentados na figura
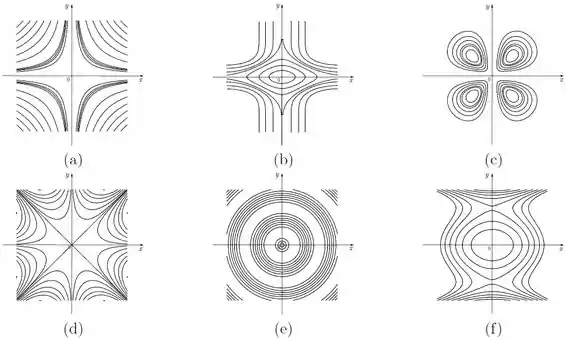
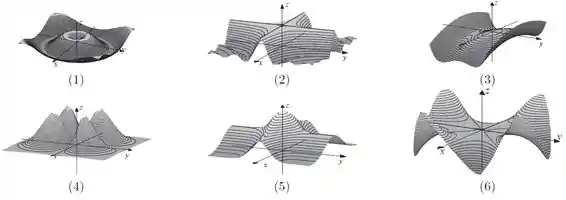
Questão 18
Os mapas de contorno abaixo (figuras , e ) correspondem a que gráficos (figura , , ou )?
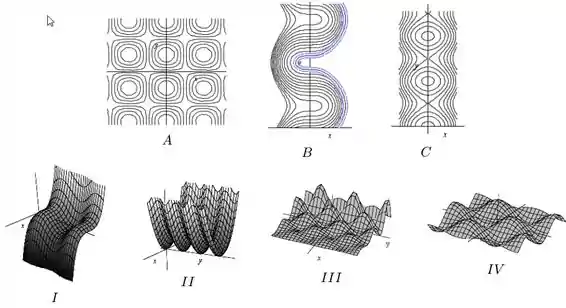
- , ,
- , ,
- , ,
- , ,
- , ,
- , ,
Questão 19
Considere as regiões do plano
Seja
- Esboce hachurado. Esboce ao lado a fronteira de , denotada por .
- Determine as constantes e as funções tal que
- Descreva o conjunto usando igualdades e desigualdades.
Questão 25
3- Desenhe as curvas de nível das funções de duas variáveis a seguir para os valores de dados:
b) ;
Ver solução completaQuestão 26
Na Figura 3 são mostradas curvas de nível para a função . Use-as para estimar o valor de e . O que você pode dizer sobre a forma do gráfico de ?
Ver solução completaQuestão 27
Nos seguintes exercícios, encontre o domínio , encontre a imagem , e descreva as curvas de nível da função:
c)
Ver solução completaQuestão 28
Considere as funções:
a) . Para quais valores de e temos ? Represente graficamente a resposta.
Ver solução completaQuestão 29
Nos seguintes exercícios, encontre o domínio , encontre a imagem , e descreva as curvas de nível da função:
e)
Ver solução completaQuestão 31
3- Desenhe as curvas de nível das funções de duas variáveis a seguir para os valores de dados:
a) ;
Ver solução completaQuestão 34
3- Desenhe as curvas de nível das funções de duas variáveis a seguir para os valores de dados:
d) ;
Ver solução completaQuestão 36
7- Dada a função , pede-se:
b) A equação e o esboço da curva de nível que contém o ponto .
Ver solução completaQuestão 37
Considere as funções:
c) . Para quais valores de e temos ? Represente graficamente a resposta.
Ver solução completaQuestão 38
Uma camada fina de metal, localizada no plano , tem temperatura no ponto . As curvas de nível de são chamadas de isotérmicas porque todos os pontos em uma isotérmica têm a mesma temperatura. Faça o esboço de algumas isotérmicas se a função de temperatura for dada por
Ver solução completaQuestão 39
Se é o potencial elétrico de um ponto do plano , as curvas de nível de são chamadas curvas equipotenciais, porque nelas todos os pontos têm o mesmo potencial elétrico. Esboce algumas curvas equipotenciais de
onde é uma constante positiva.
Ver solução completaQuestão 42
Considere a função
a) Encontre o domínio e a imagem de .
b) O gráfico de é uma superfície quádrica? Se a resposta for sim, identifique a superfície e esboce o gráfico de .
c) Identifique as curvas de nível da função e esboce um mapa de contorno. Explique a relação entre o mapa de contorno e o gráfico de
Ver solução completaQuestão 46
(Capítulo 14.2 – Exercício 37)
Determine o maior conjunto no qual a função é contínua.
Ver solução completaQuestão 47
1.4) Escreva como função das variáveis e esboce o gráfico da função
a)
b)
c)
d)
Ver solução completaQuestão 48
1.4) Escreva como função das variáveis e esboce o gráfico da função
a)
b)
c)
d)
Ver solução completaQuestão 49
1.4) Escreva como função das variáveis e esboce o gráfico da função
a)
b)
c)
d)
Ver solução completaQuestão 50
Considere a função .
- Encontre o domínio e a imagem de .
- O gráfico de é uma quádrica? Se a resposta for sim, identifique a superfície e esboce o gráfico de .
- Identifique as curvas de nível da função e esboce um mapa de contorno. Explique a relação entre o mapa de contorno e o gráfico de .
Questão 51
Resolva as questões abaixo:
- Faça o gráfico da função . Escreva uma função cuja curva de nível associado ao nível 0 é igual ao gráfico de .
- Mais geralmente, dada uma função , escreva uma função cuja curva de nível associada ao nível 0 é igual ao gráfico de . O que você pode dizer a respeito das curvas de nível de para níveis diferentes de 0?
- Seja z. Escreva uma função cuja superfície de nível associado ao nível 0 é igual ao gráfico de .
- Mais geralmente, dada uma função , escreva uma função cuja superfície de nível associada ao nível 0 é igual ao gráfico de . O que você pode dizer a respeito das curvas de nível de para níveis diferentes de 0?
Questão 53
3- Desenhe as curvas de nível das funções de duas variáveis a seguir para os valores de dados:
c) ;
Ver solução completaQuestão 56
b) Seja a superfície de equação
b1) Estude a intersecção de com cada plano e com o plano . Esboce .
b2) Encontre uma parametrização para a intersecção de com o plano .
Ver solução completaQuestão 57
(Cap. 14.1 - Ex. 46) Faça o mapa de contorno da função mostrando várias curvas de nível.
Ver solução completaQuestão 58
(Cap 14.3 – Ex 101e) Seja
(e) O resultado da parte (d) contradiz o Teorema de Clairaut? Use os gráficos de e para ilustrar sua resposta.
Ver solução completaQuestão 61
Cada uma das figuras abaixo representa uma superfície. Na coluna da tabela, temos uma equação para cada uma dessas superfícies. Cada superfície contém a imagem de uma das curvas da coluna . Escreva abaixo de cada figura qual é a curva cuja imagem está contida na superfície que ela representa: