Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Introdução à Funções Vetoriais

Ver Todos os Exercícios

Teoria

Função Vetorial

Oi, galerinhaaa! Então, vamos falar um pouco sobre vetores?! Então, lembra que a gente pode representar um vetor indicando a sua direção pelas coordenadas no eixo x e y .

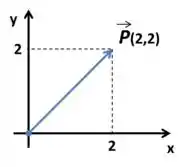
Então, em alguns casos uma função que indicará a direção desse vetor. E quando nós temos uma situação dessas, nós temos uma uma função vetorial!

Uma função vetorial de várias variáveis nada mais é do que duas (ou mais) funções de várias variáveis em um vetor, onde essas funções são as duas componentes do vetor.

Assim, para duas funções, temos:

F x , y , z = ( f x , y , z , g x , y , z )

Por exemplo:

F x , y , z = x + y + z , 2 x + y + 3 z

Agora vamos ver a notação disso!

A notação que a gente usa para funções vetoriais de várias variáveis é:

F : R n → R m    

X = x 1 , x 2 … , x n → F X = f 1 X , f 2 X , … , f m X

Relaxa, eu sei que essa notação é bizarra e parece assustadora, mas na real, nem é.

O que ela quer dizer é que temos uma função que leva n variáveis (ou parâmetros) em m coordenadas. Isso é para mostrar que uma função vetorial de várias variáveis pode levar tantos parâmetros em tantas coordenadas quanto ela quiser!

Agora vamos falar de dóminio de função vetorial de varias variáveis.

Domínio

Dominio de uma função é o conjunto em que essa função está bem definida, certo? São possíveis valores que as variáveis podem assumir. E como temos mais de uma variável, o domínio de uma função vetorial de várias variáveis será o conjunto interseção do domínio de cada uma das coordenadas dessa função, pois isso garante que, assim, todas as funções coordenadas estarão bem definidas nesse conjunto.

E pra achar o domínio de cada função coordenada é só olhar as restrições, lembrando:

  • Nas frações o denominador não pode valer 0
  • Dentro das raízes quadradas não pode ter número negativo
  • O valor dentro de um logaritmo tem que ser estritamente positivo

Então vê se você consegue me dizer o domínio dessa função:

F x , y = 25 - x 2 - y 2 , x + y

Temos

f 1 x , y = 25 - x 2 - y 2

f 2 x , y = x + y

Olhando pra f 2 a gente vê logo de cara que ela não tem restrição nenhuma, né? x e y podem ser qualquer coisa.

( x , y ) ∈ R 2

Agora, já em f 1 , temos uma raiz quadrada, então, o que tá dentro dela não pode ser um numero negativo:

25 - x 2 - y 2 ≥ 0

x 2 + y 2 ≤ 25

A interseção dessas duas restrições fica sendo

D o m F = x , y ∈ R 2   x 2 + y 2 ≤ 25 }  

E pra esboçar esse domínio, como ficaria?

Devemos pensar como se fosse uma igualdade:

x 2 + y 2 = 25

Essa equação tem uma cara conhecida! Isso seria, pela equação de uma circunferência de raio 5 centrada na origem. Lembrando que como é uma desigualdade, temos um disco de raio 5 centrado na origem, ou seja, todos os pontos estão dentro da circunferência!

Assim, nosso esboço seria:

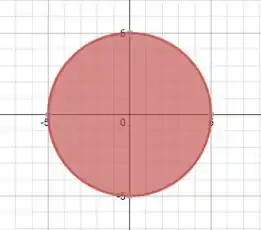
Imagem

A imagem será as nossas coordenadas, os possíveis valores que serão obtidos ao substituir a variável por um número.

Beleza, e o que fazemos para esboçar essa imagem?

Bem, para esboçar a imagem de uma função vetorial, nós precisamos encontrar uma relação entre as componentes do vetor que compõe a imagem.

No caso de uma função vetorial de uma variável. Essa relação definirá uma curva. Assim, o que precisamos é descobrir que curva é essa.

Já no caso de uma função vetorial de várias variáveis, essa relação definirá uma superfície. Então, o que precisamos é descobrir que superfície é essa.

E voialà, teremos a imagem da nossa função vetorial.

Vamos ver um exemplo pra isso ficar mais claro.

F x , y = x , y , x 2 + y 2

Observe que se chamarmos a terceira componente da função de z , temos que

z = x 2 + y 2

Essa expressão é a nossa relação entre as componentes da função vetorial. E essa relação define a parte de cima de um cone.

Assim, o esboço da nossa imagem fica

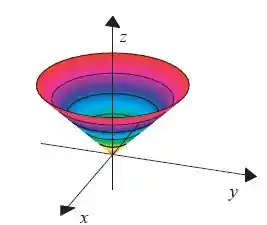
Domínio

Imagem

Exercícios Resolvidos

Exercício Resolvido #1

UFF, Cálculo 2B, Parte 1, exemplo 1.2.1

Determine e esboce o domínio da função

F x , y = 1 y   , 1 - x

Passo 1

Primeiramente vamos identificar f 1 e f 2

f 1 x , y = 1 y

f 2 x , y = 1 - x

Agora, quais são as restrições de cada uma delas?

Passo 2

Para f 1 temos uma raíz no denominador. Então sabemos que o que tem dentro da raiz tem que ser maior ou igual a zero, mas ao mesmo tempo tem que ser diferente de zero pois estão no denominador.

Assim

D o m f 1 = x , y ∈ R 2     y > 0 }

Passo 3

Para f 2 também temos uma raíz no denominador. Então sabemos que o que tem dentro da raiz tem que ser maior ou igual a zero, mas ao mesmo tempo tem que ser diferente de zero pois estão no denominador.

Assim

- x > 0

x < 0

Então

D o m f 2 = x , y ∈ R 2     x < 0 }

Passo 4

A interseção dos dois domínios fica:

D o m F = x , y ∈ R 2     x < 0   e   y > 0 }

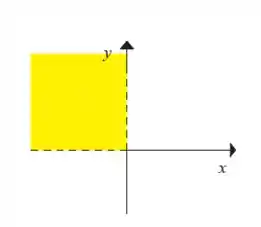
Graficamente teremos a parte do plano cartesiano em que x é negativo e y é positivo:

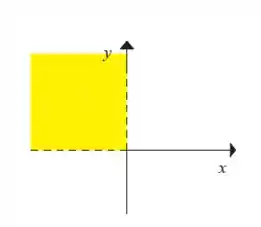
Resposta

D o m F = x , y ∈ R 2     x < 0   e   y > 0 }

Exercício Resolvido #2

UFF, Cálculo 2B, Parte 1, exemplo 1.2.2

Determine e esboce o domínio da função

F x , y = 1 1 - ( x 2 + y 2 )   , x y , y x

Passo 1

Primeiramente vamos identificar f 1 , f 2 e f 3

f 1 x , y = 1 1 - ( x 2 + y 2 )

f 2 x , y = x y

f 3 x , y = y x

Agora, quais são as restrições de cada uma delas?

Passo 2

Para f 1 temos uma raíz no denominador. Então sabemos que o que tem dentro da raiz tem que ser maior ou igual a zero, mas ao mesmo tempo tem que ser diferente de zero pois estão no denominador.

Assim

1 - x 2 + y 2 > 0

x 2 + y 2 < 1

D o m f 1 = x , y ∈ R 2     x 2 + y 2 < 1 }

Passo 3

Para f 2 temos x no numerador e y no denominador, portanto, x não tem nenhuma restrição, mas y tem que ser diferente de zero.

Assim

D o m f 2 = x , y ∈ R 2     y ≠ 0 }

Passo 4

Para f 3 temos y no numerador e x no denominador, portanto, y não tem nenhuma restrição, mas x tem que ser diferente de zero.

Assim

D o m f 3 = x , y ∈ R 2     x ≠ 0 }

Passo 5

A interseção dos dois domínios fica:

D o m F = x , y ∈ R 2     x 2 + y 2 < 1   ,   x ≠ 0   e   y ≠ 0 }

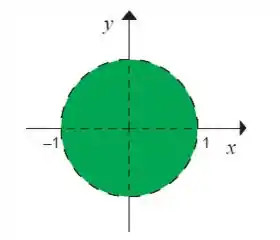
Graficamente teremos o disco x 2 + y 2 < 1 , sem as bordas, pois a desigualdade é apenas menor que 1 e sem os eixos x e y pois ambos tem que ser diferentes de zero.

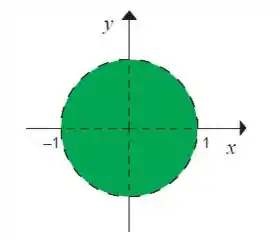
Resposta

D o m F = x , y ∈ R 2     x 2 + y 2 < 1   ,   x ≠ 0   e   y ≠ 0 }

Exercício Resolvido #3

Elaboração Própria

Determine e esboce a imagem da função vetorial

F x , y = x , y , 1 - x 2 9 + y 2 4 1 / 2

Passo 1

Nossa imagem é o vetor

F x , y = x , y , 1 - x 2 9 + y 2 4 1 / 2

Precisamos então achar uma relação entre as componentes desse vetor.

Como temos uma função vetorial de 2 variáveis, essa relação definirá uma superfície, que será a nossa imagem.

Passo 2

Observe que se chamarmos a terceira componente de z , temos

z = 1 - x 2 9 + y 2 4 1 / 2

z 2 = 1 - x 2 9 + y 2 4

E essa é a relação entre as três componentes da nossa função vetorial.

Passo 3

Maaas, ela ainda não nos diz muita coisa. Então, podemos mexer mais um pouquinho nela e vê onde chegamos.

z 2 = 1 - x 2 9 + y 2 4

x 2 9 + y 2 4 + z 2 = 1

OPA OPA! Isso ai já é alguma coisa!

E essa alguma coisa é um elipsoide, de centro na origem com focos 9 = 3 em x , 4 = 2 em y e 1 em z .

PORÉM! Repare que como na função vetorial original temos uma raiz quadrada em z, o elipsoide só vai pegar a parte positiva do eixo z.

Esboçando isso, temos:

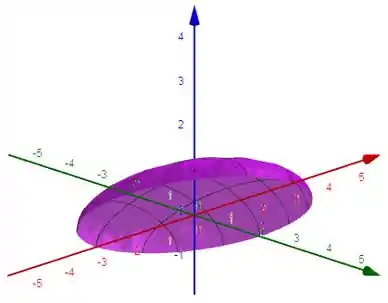
Resposta

A imagem de F é o semi-elipsoide:

x 2 9 + y 2 4 + z 2 = 1 ,   z ≥ 0

Exercícios de Livros Relacionados

Determine o domínio das funções vetoriais. r t = 4 - t ² ,e - 3 t , ln ⁡ ( t + 1 ) ²
Determine o vetor tangente unitário T(t) no ponto com valor de parâmetro dado t. r t =t e - t , 2 a r c t gt , 2 e t ,t = 0
Determine as componentes tangencial e normal do vetor aceleração. r t = e t i + 2 t j + e - t k
Sejam vec f (t) = vec a t + vec b t^2 e vec g (t) = t vec i + s e n t vec j + cos t vec k , com vec a = vec i + vec j e vec b = 2 vec i - vec j ; 0 = t = 2 pi . Calcular:(d) vec a * vec f (t) + vec b
Uma força com módulo 20 N age diretamente no sentido ascendente a partir do plano x y em um objeto com massa 4 k g . O objeto começa na origem com velocidade inicial v → 0 = i → - j → . Determine sua