Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Caso Vetorial

Ver Todos os Exercícios

Teoria

Integral de Superfície – campo vetorial

Para definirmos as integrais de superfície de campos vetoriais precisamos, antes de tudo, interpretar uma superfície de forma vetorial. Como fazer isso? Vamos tomar uma superfície S que seja regular. Definimos, em todos os pontos de S , vetores perpendiculares à superfície, gerando um campo vetorial.

Já vimos que o produto vetorial ∂ φ ∂ u × ∂ φ ∂ v representa um vetor normal à superfície parametrizada por φ ( u , v ) , certo? Assim, se quisermos um campo de vetores normais unitários, basta dividirmos essa expressão pelo módulo desse vetor, dessa forma:

n 1 → ( u , v ) = ∂ φ ∂ u × ∂ φ ∂ v   ∂ φ ∂ u × ∂ φ ∂ v  

Mas, se você pensar bem, para cada ponto, há dois vetores perpendiculares à superfície, não é? Um oposto ao outro. Nesse caso, temos dois campos vetoriais, n 1 → ( u , v ) e n 2 → ( u , v ) , com

n 1 → u , v = - n 2 → ( u , v )

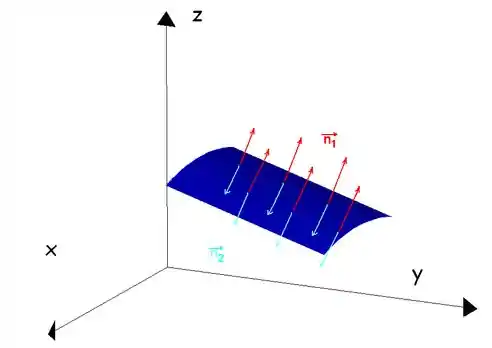
Se fixarmos sobre S um desses campos vetoriais unitários, dizemos, então que temos uma superfície orientada pelo campo vetorial n → .

Então, sendo F → um campo contínuo, definido sobre a superfície S , definimos a integral de superfície de F → sobre S dessa forma:

∬ S   F → . d S → = ∬ S   F → ⋅ n → d S

Veja que se trata de um produto escalar, portanto, resulta em um número! Essa função escalar F → ⋅ n → nos fornece a componente do campo F → na direção do vetor n → , como uma projeção.

Ótimo, agora precisamos saber como calcular essa integral, certo? Nós já vimos que o diferencial de área d S pode ser substituído por ∂ φ ∂ u × ∂ φ ∂ v   d u d v , vamos fazer isso. Substituiremos, também, a expressão que definimos para n → .

∬ S   F → . n → d S = ∬ D   F → φ u , v . ∂ φ ∂ u × ∂ φ ∂ v   ∂ φ ∂ u × ∂ φ ∂ v   ∂ φ ∂ u × ∂ φ ∂ v   d u d v

∬ S   F → . n → d S = ∬ D   F → φ u , v . ∂ φ ∂ u × ∂ φ ∂ v d u d v

Ou seja, não precisamos sempre calcular a normal unitária! A normal

N → u ,   v =   ∂ φ ∂ u × ∂ φ ∂ v

É suficiente para calcular a integral do campo F → sobre a superfície!

Na verdade, essa fórmula é muito parecida com a que vimos para as integrais de superfície escalares, a grande diferença é que não tiramos o módulo do vetor normal ∂ φ ∂ u × ∂ φ ∂ v .

Observação: Existe outra forma de escrever a integral de superfície de um campo vetorial F → , apredemos que ele é definda como

∬ S   F → ⋅ d S →

Mas, sendo o campo F → = ( F x ,   F y ,   F z ) , definimos a integral de superfície como

∬ S   ( F x d y d z + F y d z d x + F z d x d y )

Interpretação física - Fluxo

Para que serve, então, a integral de superfície de um campo vetorial?

Vamos tomar novamente a nossa superfície S e, agora, vamos imaginar um fluido escoando através dela. Suponha um campo vetorial F → que nos fornece em cada ponto a velocidade de escoamento do fluido. Queremos calcular, então, o fluxo ϕ através da superfície S .

Se analisarmos um ponto qualquer, o vetor F → possui uma componente perpendicular e uma paralela à superfície. Pelo conceito de fluxo, a taxa de escoamento por unidade de tempo, sabemos que apenas a componente perpendicular de F → contribui para o fluxo sobre S , pois representa a velocidade de entrada ou de saída do fluido. Sendo assim, faremos o produto escalar F → ⋅ n → para obter essa projeção (lembre-se de que n → é um vetor unitário).

O volume que passa através de S por unidade de tempo é dado, então, pelo produto entre essa componente da velocidade e a área da superfície:

ϕ = F → ⋅ n →   á r e a ( S )

Da mesma forma que fizemos nos capítulos anteriores, dividimos S em retalhos S i j e obtemos a Soma de Riemann. Tomando o limite dessa soma, chegamos à integral de superfície:

ϕ = lim n → ∞ ⁡ ∑ i = 1 m ∑ j = 1 n F → P i ⋅ n → P i ∆ S i j   = ∬ S   F → ⋅ n → d S

Vamos ver um exemplo agora para entender melhor isso tudo.

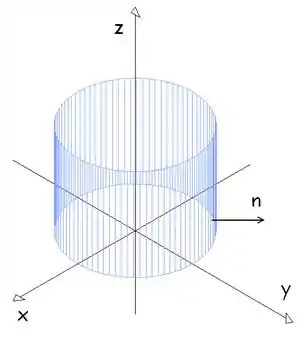
Exemplo: Calcule o fluxo ∬ S   F ⋅ n d S do campo vetorial F = ( x , y , x 2 z ) sobre a parte da superfície S dada por x 2 + y 2 = 4 que é limitada pelos planos z = 0 e z = 4 e orientada com a normal apontando para fora de S .

Passo 1: Vamos fazer um gráfico para visualizar a superfície

Temos um cilindro cortado nas alturas z = 0 e z = 4 , como podemos ver. Representamos o campo vetorial n → que orienta a superfície por um de seus vetores:

Passo 2: Parametrizar S

Como se trata de um cilindro, utilizaremos as coordenadas cilíndricas x = r cos ⁡ θ , y = r   s e n   θ e z = z . Como o seu raio é fixo r = 2 , temos:

φ θ , z = ( 2 cos ⁡ θ ,   2 sen ⁡ θ ,   z )

Onde 0 ≤ θ ≤ 2 π e 0 ≤ z ≤ 4 .

Passo 3: Calcular ∂ φ ∂ θ × ∂ φ ∂ z (nessa etapa, temos que verificar a orientação de n → )

∂ φ ∂ θ = ( - 2 sen ⁡ θ ,   2 cos ⁡ θ ,   0 )

∂ φ ∂ z = ( 0,0 , 1 )

∂ φ ∂ θ × ∂ φ ∂ z = i ^ j ^ k ^ - 2 sen ⁡ θ 2 cos ⁡ θ 0 0 0 1 = ( 2 cos ⁡ θ ,   2 sen ⁡ θ , 0 )

Agora tem uma sutileza: no caso escalar a gente tomava o módulo do vetor normal então não ligávamos para qual dos dois vetores normais estávamos escolhendo. Aqui faz diferença, mas o enunciado sempre vai nos dizer qual devemos escolher. Basta verificar se ao fazer as contas estamos escolhendo o vetor coerente com o enunciado.

Olhando para a figura, vemos que em [ 0 , π / 2 ] temos as componentes x e y do vetor positivas, o que está de acordo com ( 2 cos ⁡ θ ,   2 sen ⁡ θ , 0 ) . Se tivéssemos feito o produto ∂ φ ∂ z × ∂ φ ∂ θ encontraríamos a orientação oposta.

Passo 4: Montar a integral

∬ S   F → ⋅ n → d S = ∫ 0 4 ∫ 0 2 π F → θ , z ⋅ ( 2 cos ⁡ θ ,   2 sen ⁡ θ , 0 ) d θ d z

Escrevendo o campo em função das variáveis da parametrização, temos:

∫ 0 4 ∫ 0 2 π ( 2 cos ⁡ θ , 2 sen ⁡ θ ,   4 cos 2 ⁡ θ z ) ⋅ ( 2 cos ⁡ θ ,   2 sen ⁡ θ , 0 ) d θ d z

∫ 0 4 ∫ 0 2 π 4 cos 2 ⁡ θ + 4 sen 2 ⁡ θ d θ d z = 4 ∫ 0 4 ∫ 0 2 π   d θ d z

Passo 5: Resolver a integral

= 4 ∫ 0 4 θ 0 2 π d z =

= 8 π ∫ 0 4 d z =

= 8 π z 0 4 =

32 π

Beleza? O passo a passo para esse tipo de questão é basicamente esse aí!

Passo 1: Vamos fazer um gráfico para visualizar a superfície

Passo 2: Parametrizar S

Passo 3: Calcular ∂ φ ∂ θ × ∂ φ ∂ z , lembrar de observar a orientação de n →

Passo 4: Montar a integral

Passo 5: Resolver a integral

Bem tranquilo, né? Vamos ver uns exercícios agora pra fixar bem isso.

Interpretação física - Fluxo

Exercícios Resolvidos

Exercício Resolvido #1

Howard Anton, Irl Bivens e Stephen Davis, Cálculo – Volume II, 8ª ed. Porto Alegre: Bookman, 2007, pp. 1163 - 8

Encontre o fluxo do campo vetorial F através de σ . Onde F x ,   y ,   z = x + y i + y + z j + z + x k ; σ é a porção do plano x + y + z = 1 do primeiro octante, orientada por vetores normais unitários com componentes positivos.

Passo 1

Podemos usar a parametrização explícita para descrever nosso plano, então devemos encontrar z = f ( x , y ) :

x + y + z = 1

z = 1 - x - y  

Assim, a parametrização será:

x = u y = v z = 1 - u - v

φ u , v = ( u ,   v ,   1 - u - v )

Passo 2

Vamos calcular o vetor normal unitário a essa superfície. Para a parametrização explícita sabemos que:

N → u , v = - ∂ f ∂ u u , v ,   - ∂ f ∂ v u , v ,   1

N → u , v = 1,1 , 1

Passo 3

Agora vamos encontrar os intervalos dos parâmetros. Como é a porção do plano no primeiro octante, todas as variáveis são maiores que zero, logo:

u ≥ 0 ,   v ≥ 0

Note que as variáveis x e y variam no triângulo formado pela projeção de σ no plano x y , onde z = 0 :

z = 1 - u - v

0 = 1 - u - v

u = 1 - v

Então para cada v variando entre

0 ≤ v ≤ 1

Teremos que u   vai variar de 0 até 1 - v , que é o limite da reta, assim:

0 ≤ u ≤ 1 - v

Veja a imagem para entender melhor

Passo 4

O cálculo do fluxo é dado por:

∬ σ F . n d S

∬ σ ( u + v , 1 - u , 1 - v ) . 1,1 , 1 d u d v

∫ 0 1 ∫ 0 1 - v 2 d u d v

2 ∫ 0 1 ( 1 - v ) d v = 2 v - v 2 2 0 1 = 1

Assim, o fluxo é

∬ σ F . n d S = 1

Resposta

∬ σ F . n d S = 1

Exercício Resolvido #2

Diomara Pinto e Maria Cândida Ferreira Morgado, Cálculo Diferencial e Integral de Funções de Várias Variáveis, 3ª ed. Rio de Janeiro: UFRJ, 2009, pp. 280-6.

Calcule a integral:

∬ S F ∙ n d S

Onde:

F = - 3 x y z 2 , x + 2 y z - 2 x z 4 , y z 3 - z 2

E S é a união da superfície: x 2 + y 2 = 1

0 ≤ z ≤ 1

Com a superfície:

z = 0

x 2 + y 2 ≤ 1

Indicando a orientação escolhida para S .

Passo 1

A superfície S é a união de outras duas. Podemos então separar a integral e fazer como se fossem dois problemas: ∬ S F ∙ n d S = ∬ S 1 F ∙ n d S + ∬ S 2 F ∙ n d S

Para a primeira, que é o cilindro x 2 + y 2 = 1 , vamos parametrizar com coordenadas polares:

x = t cos ⁡ θ

y = t   s e n θ

θ ∈ 0,2 π

t > 0 Substituindo na equação da superfície:

t cos ⁡ θ 2 + t   s e n θ 2 = 1

t 2 = 1 → t = 1

x = cos ⁡ θ

y = s e n θ

Portanto z sobrou como variável, vamos torna-la um parâmetro.

ϕ θ , z = cos ⁡ θ , s e n θ , z

Jogando a parametrização nas limitações, temos simplesmente: z ∈ 0,1

Portanto nosso domínio de integração é: D 1 = z , θ ∈ R 2 θ ∈ 0,2 π ,     z ∈ 0,1

Passo 2

Encontrando o vetor normal: N = ∂ ϕ ∂ θ × ∂ ϕ ∂ z

∂ ϕ ∂ θ = - s e n θ , cos ⁡ θ , 0

∂ ϕ ∂ z = 0,0 , 1

N = i j k - s e n θ cos ⁡ θ 0 0 0 1

N = cos ⁡ θ , s e n θ , 0

Como os valores de x e y estão com um sinal positivo, o vetor normal está apontando para fora.

Passo 3

Substituindo a parametrização no campo:

F = - 3 x y z 2 , x + 2 y z - 2 x z 4 , y z 3 - z 2

F = - 3 cos ⁡ θ s e n θ z 2 , cos ⁡ θ + 2 s e n θ z - 2 c o s θ z 4 , s e n θ z 3 - z 2

Fazendo o produto escalar:

- 3 cos ⁡ θ s e n θ z 2 , cos ⁡ θ + 2 s e n ( θ ) z - 2 c o s θ z 4 , s e n θ z 3 - z 2 ∙ cos ⁡ θ , s e n θ , 0

- 3 cos 2 ⁡ θ s e n θ z 2 + cos ⁡ θ s e n θ + 2 s e n 2 ( θ ) z - 2 s e n θ cos ⁡ θ z 4

Fazendo a integral:

∬ S 1 F ∙ n d S

∬ S 1 - 3 cos 2 ⁡ θ s e n θ z 2 + cos ⁡ θ s e n θ + 2 s e n 2 ( θ ) z - 2 s e n θ cos ⁡ θ z 4   d θ d z

Substituindo os limites de integração:

∫ 0 2 π ∫ 0 1 - 3 cos 2 ⁡ θ s e n θ z 2 + cos ⁡ θ s e n θ + 2 s e n 2 θ z - 2 s e n θ cos ⁡ θ z 4 d z d θ

∫ 0 2 π - cos 2 ⁡ θ s e n θ + cos ⁡ θ s e n θ   + s e n 2 θ - 2 s e n θ cos ⁡ θ 5 d θ

∫ 0 2 π - cos 2 ⁡ θ s e n θ + 3 5 cos ⁡ θ s e n θ   + s e n 2 θ d θ

Arrumando pela fórmula trigonométrica e por substituição simples: cos ⁡ θ s e n θ = s e n 2 θ 2

v = cos ⁡ θ → d v = - s e n θ d θ

s e n 2 θ = 1 - cos ⁡ 2 θ 2

- cos 2 ⁡ θ s e n θ = v 2 d v

Substituindo:

3 5 * 1 2 ∫ 0 2 π s e n 2 θ d θ + ∫ θ = 0 θ = 2 π v 2 d v + ∫ 0 2 π 1 - cos ⁡ 2 θ 2 d θ

- 3 20 ( cos ⁡ 2 θ ) 0 2 π + v 3 3 θ = 0 θ = 2 π + π - 1 4 ( sen ⁡ 2 θ ) 0 2 π

- 3 20 cos ⁡ 4 π - cos ⁡ 0 + 1 3 cos 3 ⁡ θ 0 2 π + π - 1 4 s e n 4 π - s e n 0

- 3 20 1 - 1 + 1 3 cos 3 ⁡ 2 π - cos 3 ⁡ 0 + π - 1 4 ( 0 - 0 )

∬ S 1 F ∙ n d S = 1 3 1 - 1 + π

∬ S 1 F ∙ n d S = π

Passo 4

Fazendo a parametrização para a outra superfície, sabemos que ela é o plano z = 0 .

Com os limites:

x 2 + y 2 ≤ 1

Que é o disco de raio unitário. Parametrizamos com coordenadas polares: x = t cos ⁡ θ

y = t   s e n θ

θ ∈ 0,2 π

t > 0

Substituindo: t cos ⁡ θ 2 + t sen ⁡ θ 2 ≤ 1

t 2 ≤ 1 → 0 ≤ t ≤ 1

Portanto nossos limites são o domínio: D 2 = t , θ ∈ R 2 θ ∈ 0,2 π ,     t ∈ 0,1

Modelando o plano:

ϕ t , θ = t cos ⁡ θ , t   s e n θ , 0

Obtemos o vetor normal: N 2 = i j k cos ⁡ θ s e n θ 0 - t   s e n θ t cos ⁡ θ 0

N 2 = 0,0 , t

Para manter a ideia de vetor normal apontando para fora da superfície, precisamos apontar o vetor N 2 para baixo, logo

N 2 = 0,0 , - t

Passo 5

Fazendo a integral:

∬ S 2 F ∙ n d S

Substituímos a parametrização no campo: F = - 3 x y z 2 , x + 2 y z - 2 x z 4 , y z 3 - z 2

Não importam a primeira e a segunda coordenadas pois o produto escalar com ( 0,0 , t ) vai zerá-las. Portanto: F = ( ? , ? , t   s e n θ z 3 - z 2 )

Mas nesse plano temos z = 0 , portanto: F = ? ,   ? ,   0

Pelo produto escalar temos: F ∙ n = ? ,   ? ,   0 . 0,0 , - t = 0

Portanto a integral é nula.

∬ S 2 F ∙ n d S = 0

Resposta

∬ S F ∙ n d S = π

Com a orientação do vetor normal às superfícies apontando para fora do cilindro e para baixo do plano.

Exercício Resolvido #3

USP - Cálculo 3 - P3 2012 - 1b

Calcule

∬ S   x z   d y ∧ d z + z y 2 d z ∧ d x + y 2 2 d x ∧ d y

Onde

S = x , y , z ∈ R 3 x 2 + y 2 + z 2 = 4 ,   x 2 + y 2 ≤ 2 x ,   z ≥ 0

Orientada pela normal N → com N → . k → > 0 .

Passo 1

Antes de tudo, vamos pensar que superfície é essa do problema. Temos uma esfera x 2 + y 2 + z 2 = 4 com z ≥ 0 , portanto, apenas a casca de cima da esfera.

Temos ainda que x 2 + y 2 ≤ 2 x . Isso é a equação de um cilindro deslocado, é essa equação que limita nossa superfície no plano x y .

Nossa superfície é, portanto, a porção da casca superior da esfera que está contida dentro desse cilindro.

Passo 2

Agora vamos parametrizar essa superfíce. Vamos usar logo x e y como parâmetros, para ser mais simples:

φ x , y = ( x , y ,   4 - x 2 - y 2 )

Como ja dissemos, o que limita nossa superfície no plano x y é o cilindro, portanto, o domínio D dessa parametrização é

x 2 + y 2 ≤ 2 x

Passo 3

Agora temos que calcular a normal ∂ φ ∂ x × ∂ φ ∂ y

Temos:

∂ φ ∂ x = 1 ,   0 ,   - x 4 - x 2 - y 2

∂ φ ∂ y = ( 0,1 , - y 4 - x 2 - y 2 )

∂ φ ∂ x × ∂ φ ∂ y = i ^ j ^ k ^ 1 0 - x 4 - x 2 - y 2 0 1 - y 4 - x 2 - y 2 = x 4 - x 2 - y 2 ,   y 4 - x 2 - y 2 , 1

Bom, como o problema diz que a normal aponta para cima N → . k → > 0 , e temos a coordenada z positiva nesse vetor, sabemos que é esse mesmo o que queremos.

Passo 4

Agora, para calcular essa integral, vamos usar a seguinte fórmula:

∬ S   F → . n → d S = ∬ D   F → φ x , y ∂ φ ∂ x × ∂ φ ∂ y d x d y

Aplicando os valores que nós temos:

∬ S   F → ⋅ n → d S = ∬ D   F → φ x , y . x 4 - x 2 - y 2 ,   y 4 - x 2 - y 2 , 1 d x d y

Escrevendo o campo em função das variáveis da parametrização, temos:

x z   d y ∧ d z + z y 2 d z ∧ d x + y 2 2 d x ∧ d y

F → x , y , z = x z , z y 2 , y 2 2

φ x , y = ( x , y ,   4 - x 2 - y 2 )

F → φ x , y = x 4 - x 2 - y 2 , y 2 4 - x 2 - y 2 , y 2 2

A integral fica então

= ∬ D   x 4 - x 2 - y 2 , y 2 4 - x 2 - y 2 , y 2 2 . x 4 - x 2 - y 2 ,   y 4 - x 2 - y 2 , 1 d x d y =

= ∬ D   x 2 + y 2 2 + y 2 2 d x d y =

= ∬ D   x 2 + y 2 d x d y =

Passo 5

Beleza, agora precisamos escrever essa região D , dada por

x 2 + y 2 ≤ 2 x

Bom, como se trata de uma circunferência (onde o cilindro corta o plano x y ), vamos usar coordenadas polares:

x = r cos ⁡ θ

y = r   s e n   θ

J = r

Aplicando na nossa equação, isso nos dá

r cos ⁡ θ 2 + r   s e n   θ 2 = 2   r cos ⁡ θ

r 2 = 2 r cos ⁡ θ

r = 2 cos ⁡ θ

Essa é a equação da circunferência deslocada em coordenadas polares. Como r varia desde a origem onde r = 0 até a circunferência, temos 0 ≤ r ≤ 2 cos ⁡ θ .

Agora no intervalo de θ vamos pensar um pouquinho. Temos x 2 + y 2 = 2 x . Como o lado esquerdo dessa equação é sempre positivo (ou nulo), sabemos que 2 x ≥ 0 , logo, x ≥ 0 . Isso quer dizer que o círculo está no 1º e no 4º quadrantes do plano cartesiano.

Portanto, podemos escrever - π 2 ≤ θ ≤ π 2 .

Substituindo na integral, isso nos dá

= ∬ D   x 2 + y 2 d x d y =

= ∫ - π 2 π 2 ∫ 0 2 cos ⁡ θ r 2   r   d r   d θ =

= ∫ - π 2 π 2 ∫ 0 2 cos ⁡ θ r 3   d r d θ =

Passo 6

Agora temos que resolver isso aí

= 1 4 ∫ - π 2 π 2 r 4 0 2 cos ⁡ θ d θ =

= 4 ∫ - π 2 π 2 cos 4 ⁡ θ d θ =

Beleza, agora, precisamos usar aquela fórmula de arco duplo:

cos 2 ⁡ θ = 1 + cos ⁡ 2 θ 2

= 4 ∫ - π 2 π 2 1 + cos ⁡ 2 θ 2 2 d θ =

= ∫ - π 2 π 2 1 + 2 cos ⁡ 2 θ + cos 2 ⁡ 2 θ d θ =

Usando a fórmula mais uma vez, temos:

= ∫ - π 2 π 2 1 + 2 cos ⁡ 2 θ + 1 + cos ⁡ 4 θ 2 d θ =

= ∫ - π 2 π 2 3 2 + 2 cos ⁡ 2 θ + cos ⁡ 4 θ 2 d θ =

= 3 θ 2 + s e n   2 θ + 1 8 s e n   4 θ - π 2 π 2 =

= 3 π 4 + 0 + 0 - - 3 π 4 + 0 + 0 =

= 3 π 2

Resposta

3 π 2

Exercício Resolvido #4

USP - Cálculo 3 - P3 2010 - 1b

Calcule ∬ S   F → . N → d σ , sendo F → x , y , z = - y i → + x j → + z k → e S a parte de x 2 + y 2 + z 2 = 1 que satisfaz 2 2 ≤ z ≤ 3 2 , orientada pela normal N → tal que N → . k → > 0 .

Passo 1

Antes de tudo, vamos pensar que superfície é essa do problema. Temos uma esfera de raio 1 cortada por dois planos paralelos z = 2 2 e z = 3 2 .

A superfície S é esse pedaço da esfera entre os dois planos.

Passo 2

Agora vamos parametrizar essa superfíce em coordenadas esféricas com ρ = 1 , ok? Temos:

x = cos ⁡ θ s e n   φ

y = s e n   θ   s e n   φ

z = cos ⁡ φ

O que nos dá

σ θ , φ = ( cos ⁡ θ s e n   φ ,   s e n   θ   s e n   φ , cos ⁡ φ )

Como

2 2 ≤ z ≤ 3 2

Temos

2 2 ≤ cos ⁡ φ ≤ 3 2

Logo, φ vai de π / 6 a π / 4 .

Como temos a volta completa em torno do eixo z , 0 ≤ θ ≤ 2 π .

Passo 3

Agora temos que calcular a normal ∂ σ ∂ θ × ∂ σ ∂ φ

σ θ , φ = ( cos ⁡ θ s e n   φ ,   s e n   θ   s e n   φ , cos ⁡ φ )

Temos:

∂ σ ∂ θ = - sen ⁡ θ s e n   φ , cos ⁡ θ s e n   φ , 0

∂ σ ∂ φ = ( cos ⁡ θ cos ⁡ φ ,   s e n   θ cos ⁡ φ , - s e n   φ )

∂ σ ∂ θ × ∂ σ ∂ φ = i ^ j ^ k ^ - sen ⁡ θ s e n   φ cos ⁡ θ s e n   φ 0 cos ⁡ θ cos ⁡ φ s e n   θ cos ⁡ φ - s e n   φ =

= - s e n 2 φ cos ⁡ θ , - s e n 2 φ   s e n   θ , - cos 2 ⁡ θ s e n   φ cos ⁡ φ - s e n 2 θ   s e n   φ cos ⁡ φ =

= - s e n 2 φ cos ⁡ θ , - s e n 2 φ   s e n   θ , - s e n   φ cos ⁡ φ

Como o problema diz que a normal tal que N → . k → > 0 , precisamos inverter o sinal da normal aqui:

N → = s e n 2 φ cos ⁡ θ , s e n 2 φ   s e n   θ , s e n   φ cos ⁡ φ

Passo 4

Agora, para calcular essa integral, vamos usar a seguinte fórmula:

∬ S   F → . n → d S = ∬ D   F → σ θ , φ . ∂ σ ∂ θ × ∂ σ ∂ φ d θ d φ

Aplicando os valores que nós temos:

∬ S   F → ⋅ n → d S = ∬ D   F → σ θ , φ . s e n 2 φ cos ⁡ θ , s e n 2 φ   s e n   θ , s e n   φ cos ⁡ φ d θ d φ

Escrevendo o campo em função das variáveis da parametrização, temos:

F → x , y , z = - y , x , z

σ θ , φ = ( cos ⁡ θ s e n   φ ,   s e n   θ   s e n   φ , cos ⁡ φ )

F → σ θ , φ = - s e n   θ   s e n   φ , cos ⁡ θ s e n   φ , cos ⁡ φ

Levando para a integral

= ∬ D   - s e n   θ   s e n   φ , cos ⁡ θ s e n   φ , cos ⁡ φ . s e n 2 φ cos ⁡ θ , s e n 2 φ   s e n   θ , s e n   φ cos ⁡ φ d θ d φ =

= ∬ D   - s e n   θ cos ⁡ θ   s e n 3   φ + s e n   θ cos ⁡ θ s e n 3   φ + s e n   φ cos 2 ⁡ φ d θ d φ =

= ∬ D   s e n   φ cos 2 ⁡ φ d θ d φ =

= ∫ π 6 π 4 ∫ 0 2 π s e n   φ cos 2 ⁡ φ d θ d φ =

Passo 5

Agora vamos resolver isso aí

= 2 π ∫ π 6 π 4 s e n   φ cos 2 ⁡ φ d φ =

= - 2 π 3 cos 3 ⁡ φ π 6 π 4 =

= - 2 π 3 2 2 8 - 3 3 8 =

= π 12 3 3 - 2 2

Resposta

π 12 3 3 - 2 2

Exercício Resolvido #5

UFRJ - Cálculo 3 - PF 2014.2 – 3

Seja S a superfície de revolução obtida girando a curva C , definida pela equação

y = e x ,             x ∈ [ 0,1 ]

Em torno do eixo O X com vetor normal apontando para o lado do eixo de revolução. Calcule o fluxo do campo vetorial

F → x , y , z = x z 2 + y 2 , y , z

Através da superfície de revolução S .

Passo 1

O problema nos pede o seguinte:

∬ S   F . n d S

Então, antes de tudo, vamos descobrir quem é S . Podemos parametrizar a curva que gera S como:

γ x = x , e x ,           x ∈ [ 0,1 ]

Lembra daquele macete para parametrizar superfície de revolução?

Sendo γ uma curva do plano x y parametrizada por γ x , a parametrização da superfície gerada quando rotacionamos γ em torno do eixo x é:

φ θ , x = x x ,   y x cos ⁡ θ , y x sen ⁡ θ

φ θ , x = x ,   e x cos ⁡ θ , e x sen ⁡ θ

Em resumo: a variável x , paralela ao eixo de rotação não se altera: x = x ( t ) .

As outras duas variáveis serão escritas em função de y ( x ) , a coordenada da parametrização da curva que nos restou. Como y é pertencente ao plano da curva, apresentará cos ⁡ θ ; e z , não pertencente, apresentará sen ⁡ θ .

Como temos uma volta completa:

0 ≤ θ ≤ 2 π

Foi?

Passo 2

Agora nós precisamos da normal a S :

φ θ , x = x ,   e x cos ⁡ θ , e x sen ⁡ θ

∂ φ ∂ x = 1 ,   e x cos ⁡ θ , e x sen ⁡ θ

∂ φ ∂ θ = 0 ,   - e x s e n   θ , e x cos ⁡ θ

∂ φ ∂ x × ∂ φ ∂ θ = i j k 1 e x cos ⁡ θ e x sen ⁡ θ 0 - e x s e n   θ e x cos ⁡ θ = e 2 x , - e x cos ⁡ θ , - e x s e n   θ

Agora imagine essa curva girando em torno do eixo O X :

Para a normal apontar para esse eixo, ou seja, para dentro de S , a componente x da nomal deve ser positiva, percebeu? Isso porque a normal deve estar inclinada para a direita no gráfico.

Então, sabemos que o vetor que queremos é o mesmo que encontramos.

Passo 3

Vamos, então, usar a fórmula:

∬ S   F → . n → d S = ∬ D   F → φ x , θ . ∂ φ ∂ θ × ∂ φ ∂ x d x d θ

F → φ x , θ = x e 2 x , e x cos ⁡ θ , e x sen ⁡ θ

Isso nos dá

= ∫ 0 2 π ∫ 0 1 x e 2 x , e x cos ⁡ θ , e x sen ⁡ θ . e 2 x , - e x cos ⁡ θ , - e x s e n   θ d x d θ =

= ∫ 0 2 π ∫ 0 1 x - e 2 x cos 2 ⁡ θ - e 2 x s e n 2 θ d x d θ =

= ∫ 0 2 π ∫ 0 1 x - e 2 x d x d θ =

= ∫ 0 2 π x 2 2 - 1 2 e 2 x 0 1 d θ =

= ∫ 0 2 π 1 2 - 1 2 e 2 - 0 - 1 2 d θ

= ∫ 0 2 π 1 - e 2 2 d θ

= π 2 - e 2

Resposta

π 2 - e 2

Exercício Resolvido #6

USP - Cálculo 3 - PSUB 2015 – 3

Calcule ∬ S   F → . N → d S onde F → x , y , z = r → r → 3 → e S é a parte do hiperboloide x 2 + y 2 - z 2 = 1 limitado pela esfera x 2 + y 2 + z 2 = 2 com a normal que aponta no sentido que se afasta do eixo z .

Passo 1

Antes de tudo, vamos pensar que superfície é essa do problema. Temos um hiperboloide cortado por uma esfera:

A superfície do problema é a parte do hiperboloide que está dentro da esfera, portanto, isso aqui:

Onde a normal aponta para fora.

Passo 2

Como temos simetria em relação ao eixo z e termos quadráticos, vamos parametrizar essa superfície em coordenadas cilíndricas, ok? Temos:

x = r cos ⁡ θ

y = r   s e n   θ

z = z

O que nos dá

x 2 + y 2 - z 2 = 1

r 2 - z 2 = 1

z = ± r 2 - 1

φ 1 r , θ = ( r cos ⁡ θ ,   r   s e n   θ , r 2 - 1 )

φ 2 r , θ = ( r cos ⁡ θ ,   r   s e n   θ , - r 2 - 1 )

Temos duas parametrizações muito parecidas, uma para a parte do hiperboloide que fica acima do plano x y e outra para a parte que fica abaixo.

OBS: Essas duas superfícies são simétricas em z . Se você reparar, a função que vamos integrar F → x , y , z = r → r → 3 → também é simétrica em z , o que quer dizer que a integral sobre φ 1 vai ser igual �� sobre φ 2 . Por isso, vamos trabalhar aqui só com φ 1 e dobrar o resultado, ok?

Como temos a volta completa em torno do eixo z , 0 ≤ θ ≤ 2 π . Para descobrir o intervalo de r precisamos descobrir onde o hiperboloide corta a esfera:

x 2 + y 2 - z 2 = 1

x 2 + y 2 + z 2 = 2

Somando as duas equações, temos:

2 x 2 + 2 y 2 = 3

x 2 + y 2 = 3 2

Sabemos então que as superfícies se cortam em r = 3 / 2 , certo?

Como o raio mínimo é r = 1 , quando z = 0 , nós sabemos que 1 ≤ r ≤ 3 / 2 .

Passo 3

Agora temos que calcular a normal ∂ φ 1 ∂ r × ∂ φ 1 ∂ θ

φ 1 r , θ = ( r cos ⁡ θ ,   r   s e n   θ , r 2 - 1 )

Temos:

∂ φ 1 ∂ r = cos ⁡ θ , s e n   θ , r r 2 - 1

∂ φ 1 ∂ θ = ( - r   s e n   θ , r cos ⁡ θ , 0 )

∂ φ 1 ∂ r × ∂ φ 1 ∂ θ = i ^ j ^ k ^ cos ⁡ θ s e n   θ r r 2 - 1 - r   s e n   θ r cos ⁡ θ 0

= - r 2 r 2 - 1 cos ⁡ θ , - r 2 r 2 - 1   s e n   θ , r cos 2 ⁡ θ + r   s e n 2 θ =

= - r 2 r 2 - 1 cos ⁡ θ , - r 2 r 2 - 1   s e n   θ , r

Bom, como o problema diz que a normal aponta para longe de z , isso quer dizer, para φ 1 , a componente z da normal ser negativa. Volta lá no desenho se você ficou confuso. Logo, o vetor que queremos é o oposto a esse:

∂ φ 1 ∂ θ × ∂ φ 1 ∂ r = r 2 r 2 - 1 cos ⁡ θ , r 2 r 2 - 1   s e n   θ , - r

Passo 4

Agora, para calcular essa integral, vamos usar a seguinte fórmula:

∬ S   F → . n → d S = ∬ D   F → φ r , θ ∂ φ ∂ r × ∂ φ ∂ θ d r d θ

Como nós vimos que a integral em φ 1 vai ser igual à em φ 2 , temos:

∬ S   F → . n → d S = 2 ∬ D   F → φ 1 r , θ ∂ φ 1 ∂ r × ∂ φ 1 ∂ θ d r d θ

Aplicando os valores que nós temos:

∬ S   F → ⋅ n → d S = 2 ∬ D   F → φ r , θ . cos ⁡ θ , s e n   θ , 2 r r 2 - 1 d r d θ

Onde

F → x , y , z = r → r → 3 → = 1 x 2 + y 2 + z 2 3 / 2 ( x , y , z )

Escrevendo nas variáveis da parametrização:

F → φ r , θ = r cos ⁡ θ ,   r sen ⁡ θ , r 2 - 1 r 2 cos 2 ⁡ θ + r 2 sen 2 ⁡ θ + r 2 - 1 3 / 2 = r cos ⁡ θ ,   r sen ⁡ θ , r 2 - 1 2 r 2 - 1 3 / 2

= 2 ∬ D   r cos ⁡ θ ,   r sen ⁡ θ , r 2 - 1 2 r 2 - 1 3 / 2 . cos ⁡ θ , s e n   θ , 2 r r 2 - 1 d r d θ =

= 2 ∬ D   r + 2 r 2 r 2 - 1 3 / 2 d r d θ =

= 6 ∬ D   r 2 r 2 - 1 3 / 2 d r d θ =

Trazendo os intervalos de r e θ :

= 6 ∫ 0 2 π ∫ 1 3 / 2 r 2 r 2 - 1 3 / 2 d r d θ =

Passo 5

Agora vamos resolver isso aí. Fazendo:

2 r 2 - 1 = u

4 r d r = d u

r = 3 2           →             u = 2

r = 1           →             u = 1

= 6 4 ∫ 0 2 π ∫ 1 2 1 u 3 / 2 d u d θ =

= 3 ∫ 0 2 π 1 u 1 2 d θ =

= 3 ∫ 0 2 π 1 2 - 1 d θ =

= 6 π 1 2 - 1

Resposta

6 π 1 2 - 1

Exercícios de Livros Relacionados

Calcule a integral de superfície ∫ ∫ SF ∙ d S para o campo vetorial F e superfície orientada S . Em outras palavras, determine o fluxo de F através de S . Para superfícies fechadas, use a orientação p
Calcule a integral de superfície ∫ ∫ SF ∙ d S para o campo vetorial F e superfície orientada S . Em outras palavras, determine o fluxo de F através de S . Para superfícies fechadas, use a orientação p
A temperatura de um ponto da bola com condutividade K é inversamente proporcional à distância do centro da bola. Determine a taxa de transmissão de calor através de uma esfera S de raio a e centro da
Determine uma fórmula para ∬ S F → ⋅ d S → semelhante à fórmula 10 para o caso onde S é dado por y = h ( x , z ) e n → é o vetor normal unitário que aponta para a esquerda.
Determine uma fórmula para ∬ S F → ⋅ d S → semelhante à fórmula 10 para o caso onde S é dado por x = h ( y , z ) e n → é o vetor normal unitário que aponta para frente (ou seja, para o observador, qua