Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Teorema de Stoke

Ver Todos os Exercícios

Teoria

Fala aí! Seja bem vindo ao Responde Aí! Bora aprender o que é o Teorema de Stokes e como utilizá-lo de uma vez por todas?

O que é o Teorema de Stokes?

O Teorema de Stokes relaciona uma integral de linha com uma integral de superfície, ela funciona como uma versão 3D do Teorema de Green!

Então, sem mais enrolação, o enunciado do Teorema de Stokes é o seguinte:

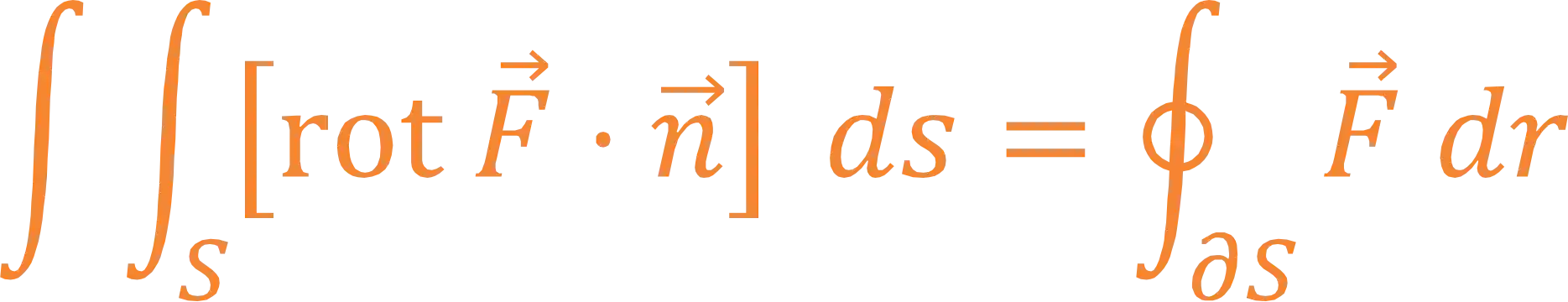
Sendo uma superfície orientada positivamente, se é um campo vetorial definido em todo domínio de integração e se a fronteira de , que chamaremos de está orientada positivamente, pelo Teorema de Stokes:

Teorema de Stokes
Teorema de Stokes

Calma, calma, vamos entender todos os detalhes desse teorema aqui! Destacamos alguns termos que são as hipóteses do teorema!

Hipóteses do Teorema de Stokes

  1. A curva da integral de linha é a fronteira de , ou seja, é uma curva fechada!
  2. O campo é definido em todos os pontos do domínio, ou seja, não podemos ter singularidades!
  3. A superfície deve ser orientada positivamente.

Essas são as condições necessárias para o funcionamento correto do teorema de Stokes, então vamos fazer um exemplo para ficar tudo mais claro!

📢 Clique para saber mais:

Exemplo: Sendo a curva dada pela interseção do paraboloide com o semicone orientada no sentido horário quando observada a partir da origem dos eixos coordenados, calcule:

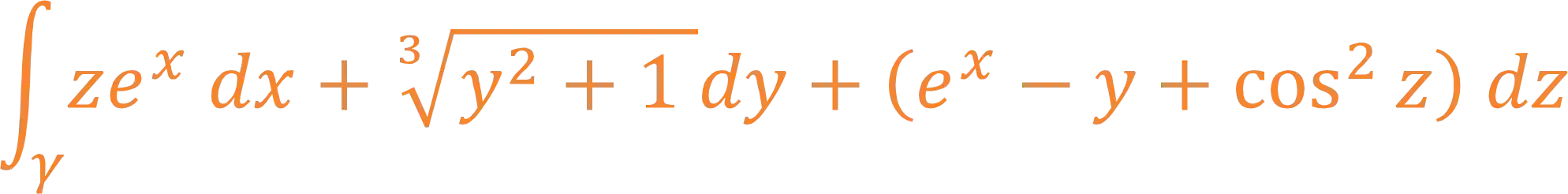
Teorema de Stokes: Exemplo
Teorema de Stokes: Exemplo

Passo 1: Fazer o Gráfico da Região

Primeira coisa que vamos perceber é que temos uma integral de linha no e que é muito difícil resolvê-la pelo método direto (imagina se tivéssemos que parametrizar isso), então por isso vamos utilizar o Teorema de Stokes.

Para começar vamos fazer um gráfico da região:

Gráfico da região
Gráfico da região

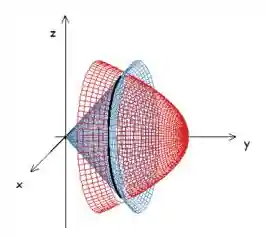
Repare que o que queremos descobrir é a interseção entre as duas curvas, que como vemos no gráfico forma um circulo, que teve seu perímetro pintado de preto na figura. Como é curva fechada, é muito melhor usar o teorema de Stokes, ao invés de parametrizar a curva.

Passo 2: Calcular o Vetor Rotacional

Vamos entender agora, como utilizar o teorema de Stokes para curvas fechadas e utilizá-lo para calcular a circulação da figura do gráfico.

Para isso precisaremos calcular esse termo que representa o campo vetorial rotacional de , que chamamos muitas vezes de rotacional de . Vamos descobrir seu valor a partir do produto vetorial:

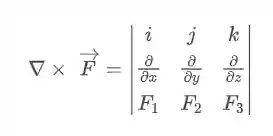
Vetor rotacional
Vetor rotacional

Sabendo que:

Podemos calcular as derivadas parciais e descobrir que:

Você também pode conferir o resto dessa resolução no vídeo abaixo!

Passo 3: Encontrar a Expressão que Representa a Curva

Nosso vetor rotacional até que ficou bem simples né? Mais um indicio que calcular essa integral usando o método de Stokes deve ser melhor que pela definição de integral de linha. Então agora vamos encontrar a expressão que representa a curva . Vamos descobrir a interseção das superfícies manipulando as equações da seguinte forma:

Isolamos e agora podemos substituir na equação da segunda superfície:

Elevando os dois lados ao quadrado e reorganizando a expressão:

E está ai a equação da nossa curva, resolvendo essa equação encontramos e como a curva está na parte positiva do eixo , temos que utilizar , logo:

E então podemos concluir que nossa curva é uma figura de uma circunferência paralela ao plano em e raio igual a 1.

Passo 4: Calcular a Circulação Usando o Teorema de Stokes

Agora que já sabemos o formato da figura e onde ela se encontra podemos definir nossa superfície e parametrizá-la. Dessa forma vamos escolher um circulo contido no plano , e vamos calcular sua circulação utilizando o teorema de Stokes

Agora temos que nos preocupar com o vetor normal, que no caso ficará paralelo ao eixo , como fixamos o valor de vamos variar apenas os valores de e e podemos escrever nossa parametrização com a seguinte cara:

Com .

Passo 5: Achar o Vetor

Agora temos que descobrir o valor do vetor , para isso vamos precisar dos valores da derivada parcial da nossa parametrização em relação a e em relação a :

E agora podemos calcular o seguinte produto vetorial, para encontrar o valor do vetor normal:

E isso coincide com nossas predições que o vetor normal, deve ser paralelo ao eixo :

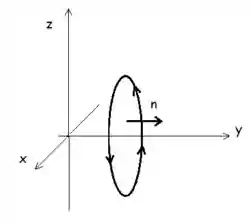
Vetor n
Vetor n

Passo 6: Aplicar o Teorema de Stokes

E agora finalmente podemos aplicar o teorema e encontrar o resultado:

Á

Como é um círculo de raio 1, temos:

Á

Portanto o resultado de nossa circulação vale:

Exercício: Usando o teorema de Stokes, calcule o trabalho realizado pelo campo de forças

Quando uma partícula se move sob sua influência ao longo da curva de interseção das superfícies  e  , orientada no sentido anti-horário quando vista de cima.

Agora vamos praticar com mais exercícios?

Exercício: Usando o teorema de Stokes, calcule o trabalho realizado pelo campo de forças

Exercícios Resolvidos

Exercício Resolvido #1

George B. Thomas e Weir Hass Giordano, Cálculo –Volume 2, 11ª ed. São Paulo: Pearson Education Brasil ltda., 2009, pp. 534 - 3

Use a integral de superfície no teorema de Stokes para calcular a circulação do campo F   ao redor da curva C no sentido indicado.

F : y i + x z j + x 2 k

C : A fronteira do triângulo cortado a partir do plano x + y + z = 1 pelo primeiro octante, no sentido anti-horário quando vista de cima.

Passo 1

Antes de aplicar o Teorema de Stokes vamos ver o que é circulação. Circulação é definido como:

∮ ∂ S   F → . d r

Que sorte! Porque o Teorema de Stokes nos diz que:

∮ ∂ S   F → . d r = ∬ S   ( ∇ ×   F ) → . n → d S

Passo 2

Vamos começar calculando o rotacional de F :

∇ ×   F → = i j k ∂ ∂ x ∂ ∂ y ∂ ∂ z F 1 F 2 F 3

∇ ×   F → = ( - x , - 2 x , z - 1 )

Passo 3

Para este plano podemos usar a parametrização explícita:

z = f x , y = 1 - x - y

N → x , y = - ∂ f ∂ x x , y ,   - ∂ f ∂ y x , y ,   1

N → x , y = 1 ,   1 ,   1

Passo 4

Resolvendo a integral de superfície:

∮ ∂ S   F → . d r =   ∬ σ ( ∇ ×   F → ) . n → d S = ∬ σ ( ∇ ×   F → ) . N → d x d y

∬ σ ( - x , - 2 x , z - 1 ) . 1 ,   1 ,   1 d y d x

∫ 0 1 ∫ 0 1 - x - x - 2 x + z - 1   d y d x

Como, z = 1 - x - y

∫ 0 1 ∫ 0 1 - x - 4 x - y d y d x

∫ 0 1 - 4 x 1 - x + 1 2 1 - x 2 d x

- ∫ 0 1 1 2 + 3 x - 7 2 x 2 d x = - 5 6

Resposta

Assim, temos que a circulação

∮ ∂ S   F → . d r = - 5 6

Exercício Resolvido #2

UFF - Cálculo IIIA - P2 Maria João 2014.1 – 5

Usando o teorema de Stokes, calcule o trabalho realizado pelo campo de forças

F → = z - y ,   - x - z ,   - x - y

quando uma partícula se move sob sua influência ao longo da curva de interseção das superfícies x 2 + y 2 + z 2 = 4 e z = y , orientada no sentido anti-horário quando vista de cima.

Passo 1

Galerinha, a gente começa relembrando um pouco lá da física, onde trabalho é força vezes o deslocamento. Então, neste caso, podemos escrever o trabalho W dessa forma aqui:

W = ∫ C F → . d r →

Para resolver essa integral vamos utilizar o Teorema de Stokes. Então teremos essa igualdade aqui:

W = ∫ C F → . d r → = ∬ S   r o t   F →   . n →   d s

Onde a curva C é o bordo da superfície S orientada positivamente.

Passo 2

A gente vai começar, esboçando essas superfícies para entender melhor o problema.

O enunciado forneceu a equação de duas superfícies.

A primeira é a equação da esfera, cujo raio é 2 :

x 2 + y 2 + z 2 = 4

Já a segunda equação é um plano:

z = y

Esboçando as duas curvas, temos:

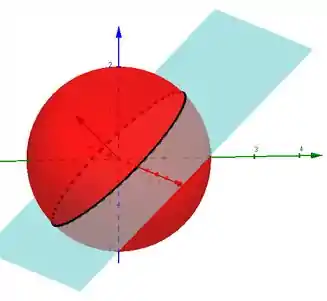
A interseção da esfera com o plano é uma elipse. Para achar essa elipse, basta substituir a equação do plano ( z = y ) na equação da esfera:

x 2 + y 2 + y 2 = 4

x 2 + 2 y 2 = 4

Dividindo tudo por 4 , para se encaixar na equação geral da elipse:

x 2 4 + y 2 2 = 1

Beleza?? Essa é a nossa elipse que será a interseção entre o plano e a esfera!

O enunciado também diz que ela está orientada no sentido anti-horário vista de cima. Deste modo, pela regra da mão direita, podemos ver que o vetor normal à superfície S deve estar apontando para cima para aplicarmos o teorema de Stokes.

Passo 3

Agora vamos partir para integral!

W = ∬ S   r o t   F →   . n →   d s

Precisamos do rotacional do campo F → ! O rotacional é dado por:

r o t F → = ∂ F 3 ∂ y - ∂ F 2 ∂ z ,   ∂ F 1 ∂ z - ∂ F 3 ∂ x ,   ∂ F 2 ∂ x - ∂ F 1 ∂ y

Como nosso campo F → é

F → = z - y ,   - x - z ,   - x - y

Temos que,

F 1 = z - y

F 2 = - x - z

F 3 = - x - y

Calculando, ficamos com

r o t F → = - 1 - - 1 ,   1 - - 1 ,   - 1 - - 1

r o t F → = 0 ,   2 ,   0

Passo 4

Repara que na nossa integral temos o rotacional é multiplicado pelo vetor normal!

Então, precisamos do vetor normal à superfície S .

Observando o esboço da superfície, vemos que a elipse que queremos orientar está contida no plano - y + z = 0 . Se não ficou claro, é só reparar que o o vetor normal sai do centro e avança para valores de y negativos e z positivos. Aahh, repara que ele não tem componente em x .

Escrevendo na forma vetorial, temos

N → = 0 ,   - 1 ,   1

Ele é um vetor normal à superfície sobre a qual estamos integrando com a orientação que queremos.

Passo 5

Já temos todos os elementos, vamos para integral! Ela fica assim:

W = ∫ C F → . d r → = ∬ S   r o t   F →   . n →   d s = ∬ S 0 ,   2 ,   0   . 0 ,   - 1 ,   1   d s = ∬ S - 2   d s

W = ∬ S - 2   d s

Então, temos que achar a área da superfície formada pela interseção do plano com a esfera. Como já vimos, nossa superfície é a elipse:

x 2 4 + y 2 2 = 1

Como a equação geral da elipse é:

( x - x 0 ) 2 a 2 + ( y - y 0 ) 2 b 2 = 1

Temos, aqui, a = 2 e b = 2 .

Então, basta a gente calcular a área dessa elipse, que é dada por a b π :

A r e a S = 2 2 π = 2 2 π

Dessa forma, podemos substituir em W :

W = - 2 ⋅ A r e a S = - 4 2 π

Logo, esse é o valor do trabalho pedido na questão! 😊

Resposta

- 4 2 π

Exercício Resolvido #3

Diomara Pinto e Maria Cândida Ferreira Morgado, Cálculo Diferencial e Integral de Funções de Várias Variáveis, 3ª ed. Rio de Janeiro: UFRJ, 2009, pp. 293 - 5.

Use o teorema de Stokes para mostrar que a integral de linha é igual ao valor dado, indicando a orientação da curva C .

∮ C   8 x - 2 y d x + y d y + 3 z d z = 4 3

onde C é a fronteirado triângulo equilátero situado no plano - 3 x + 3 z + 6 = 0 de vértices P = 2,2 , 0 ,   Q = ( 2,6 , 0 ) e R = ( 2 + 3 , 4,3 )

Passo 1

Primeiro devemos encontrar a função vetorial em questão e o seu rotacional. Temos que F → = ( 8 x - 2 y ,   y ,   3 z ) e o rotacional pode ser calculado por:

∇ ×   F → = i j k ∂ ∂ x ∂ ∂ y ∂ ∂ z F 1 F 2 F 3

∇ ×   F → = ( 0 ,   0 ,   2 )

Passo 2

Agora vamos encontrar a normal a superfície, esta superfície pode ser parametrizada de forma explícita como:

z = f x , y = 3 x - 6 3

Assim,

N → x , y = - ∂ f ∂ x x , y ,   - ∂ f ∂ y x , y ,   1

N → x , y = - 3 3 ,   0 ,   1

Passo 3

Vamos aplicar o teorema de Stokes ∮ ∂ S   F → . d r = ∬ S   ∇ ×   F → . n → d S = ∬ S   ∇ ×   F → . N → d x d y

Substituindo pelo rotacional e pela normal que calculamos, temos:

∬ S   ∇ ×   F → . N → d x d y =   ∬ S   0,0 , 2 . - 3 3 ,   0 ,   1 d x d y = ∬ S   2 d x d y

Mas, ∬ S   2 d x d y , representa o dobro da área da superfície projetada no plano x y . Não confunda isso! Quando temos “ d x d y ” ali do lado, estamos falando de tudo no plano x y já, beleza?

Passo 4

O último passo é calcular a área da superfície! Sorte nossa que é um triângulo! Esse aqui é o triângulo original da questão, ele está em 3 D :

R = 2 + 3 , 4,0

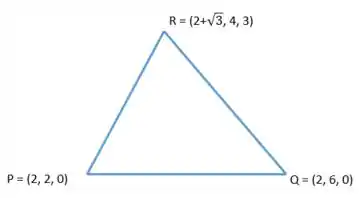
Precisamos projetar ele no plano x y pra calcular a área, mas isso é simples: só zerar os termos em z . No caso fica assim

R ' = 2 + 3 , 4

P = 2,2

Q = 2,6

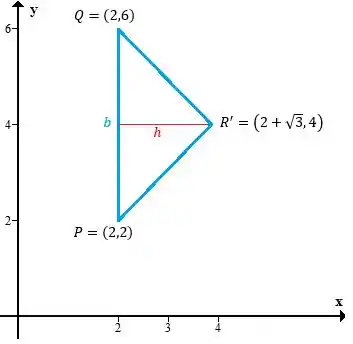
O lado P Q tem medida igual a 4 pois os dois pontos estão no plano x y e sobre a reta x = 2 , então a distância entre eles é a diferença entre a coordenada y .

A altura aqui também está sobre a reta y = 4 , portanto o seu tamanho vai ser dado pela diferença nas coordenadas de x , logo h = 2 + 3 - 2

h = 3

Logo, a área do triângulo é:

A = b h 2

A = 4 . 3 2 = 2 3

Então,

2 A = 4 3

E aproveitando a imagem aí em cima e sabendo que a normal que escolhemos aponta para o x negativo, nós temos a orientação da curva C ! Que no caso é Q → P → R → Q .

Resposta

Assim, a integral de linha do camp F → definido no enunciado é dada por:

∮ C   F → . d r = 2 A = 4 3

E a orientação usada foi Q → P → R → Q

Exercício Resolvido #4

UERJ - Análise Vetorial - Lista 4 Flávio - 3ª

Utilizando o Teorema de Stokes, transforme a integral ∬ S   r o t F .   n →   d s numa integral de linha e a calcule, sabendo que F x , y , z = ( 0,0 , y ) , S é parametrizada por φ u , v = ( u , v , u 2 + v 2 ) , com u 2 + v 2 ≤ 1 , sendo n → a normal apontando para cima.

Passo 1

Antes de tudo vamos fazer um gráfico da região para entender melhor a questão. A parametrização φ u , v = ( u ⏟ x , v ⏟ y , u 2 + v 2 ⏟ z ) nos diz que:

z = x 2 + y 2

Ou seja, um paraboloide, certo? Mas algo tem que limitar essa superfície, senão ela é infinita. Nós temos que

u 2 + v 2 ≤ 1

Ou seja,

x 2 + y 2 ≤ 1

Isso nos diz que o domínio dessa superfície é o círculo de raio 1 centrado na origem. Portanto, temos isso aqui:

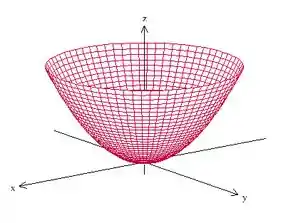
E o Teorema de Stokes nos diz o seguinte:

∬ S   r o t F → . n → d s = ∮ ∂ S   F → . d r

Ou seja, podemos substituir essa integral do rotacional de F na superfície S por uma integral de linha sobre a fronteira de S . Como podemos ver pela imagem, essa fronteira é uma circunferência de raio 1 .

Passo 2

Certo, agora precisamos calcular essa integral de linha. Como nós já estamos cansados de ver, o primeiro passo agora é achar uma parametrização para essa curva.

Bom, como se trata de uma circunferência de raio 1 , temos que

x 2 + y 2 = 1

Precisamos agora definir a coordenada z dessa curva, ou seja, a altura da circunferência. Como ela faz parte do paraboloide, nada mais justo que substituir sua equação na dele, certo?

z = x 2 + y 2 = 1

z = 1

Pronto, descobrimos a altura dessa curva, agora precisamos parametrizá-la. Como se trata de uma circunferência, a melhor saída aqui é usar coordenadas polares

x = r cos ⁡ θ

y = r   s e n   θ

Como sabemos que o raio é igual a 1 , podemos substituir r = 1 . Como é dada uma volta completa temos 0 ≤ θ ≤ 2 π . Lembrando que o z é fixo em z = 1 . Isso nos dá:

σ → θ = ( cos ⁡ θ ,   s e n   θ ,   1 )

0 ≤ θ ≤ 2 π

Passo 3

Agora precisamos calcular a derivada dessa parametrização:

σ → ' θ = ( - s e n   θ , cos ⁡ θ ,   0 )

Passo 4

Vamos, então, substituir σ → ' θ na fórmula abaixo e escrever F em função do parâmetro θ

∫ γ   F . d r = ∫ a b F x θ ,   y θ , z ( θ ) . σ → ' θ d θ

Escrevendo a função vetorial

F x , y , z = 0,0 , y

Em termos da parametrização

σ → θ = ( cos ⁡ θ ,   s e n   θ ,   1 )

Temos

F x θ , y θ , z ( θ ) = 0 , 0 , s e n   θ

Substituindo na fórmula, temos

∫ γ   F . d r = ∫ 0 2 π 0 , 0 , s e n   θ . - s e n   θ , cos ⁡ θ ,   0 d θ =

= ∫ 0 2 π 0 d θ = 0

Resposta

0

Exercício Resolvido #5

UFRJ, Cálculo III, P2/2011.1, 3

Seja C a curva orientada parametrizada por:

r → t = cos ⁡ t , s e n t , 8 - cos 2 ⁡ t - s e n t

t ∈ 0,2 π

Seja o campo vetorial:

F → = z 2 - y 2 , - 2 x y 2 , e z cos ⁡ z

Calcule:

∫ C   F ∙ d r

Passo 1

Pela cara do campo vetorial, devemos aplicar Stokes, pois resolver a integral de linha pela sua definição não seria agradável.

O campo F é de classe C ∞ se z > 0 por causa daquele expoente z . Portanto temos que, pela Lei de Stokes: r o t F = 0,2 z , - 2 y 2 + 2 y

Analisando a curva C , vemos que z t > 6 para todo t ∈ 0,2 π .

Isso porque o valor máximo de um seno ou cosseno é 1 ! Então na coordenada z temos no mínimo 8 - 1 - 1 = 6 !

Claro que cosseno e seno nunca valem 1 ao mesmo tempo então o limite inferior para z seria até um pouco maior que 6 , mas o que importa é que ele seja maior que 0 pra não dar zica naquela raiz!

Substituindo por coordenadas cartesianas, temos que a curva está contida na superfície:

z = 8 - x 2 - y

Vamos utilizar essa superfície na formula de Stokes.

Passo 2

Observamos que a projeção da curva C no plano coordenado x y (zerando a coordenada z ) é um círculo de raio 1 e tem o sentido anti-horário. Portanto, orientamos a superfície de forma compatível com o teorema de Stokes, isto é, com a terceira componente do vetor normal sendo positiva. Usando a parametrização natural, isto é:

ϕ x , y = x , y , 8 - x 2 - y

Temos que o domínio D da parametrização é dado por:

x 2 + y 2 ≤ 1

Temos também que o vetor normal é:

N = ∂ ϕ ∂ x × ∂ ϕ ∂ y

N = 2 x , 1,1

Que tem a orientação desejada.

Passo 3

Segue que:

r o t F = 0,16 - 2 x 2 - 2 y , - 2 y 2 + 2 y

r o t F ∙ N = 16 - 2 x 2 + y 2

Aplicando Stokes:

∫ C   F ∙ d r = ∬ D   16 - 2 ( x 2 + y 2 ) d x d y

Aplicando coordenadas polares por causa do domínio e da integral:

x = r cos ⁡ θ

y = r   s e n θ

θ ∈ 0,2 π

Plugando a parametrização na definição do domínio D :

r cos ⁡ θ 2 + r   s e n   θ 2 ≤ 1

r 2 ≤ 1 → 0 ≤ r ≤ 1

Isto pois r é positivo por definição.

Agora mudemos os diferenciais por jacobiano:

d x d y = r   d r d θ

Passo 4

Plugando os limites e a parametrização na integral:

∫ C   F ∙ d r = ∫ 0 2 π ∫ 0 1 16 r - 2 r 3 d r d θ

Em θ a integral é moleza, a outra é só um polinômio. Partiu pro abraço:

∫ C   F ∙ d r = 2 π 8 r 2 - r 4 2 0 1

∫ C   F ∙ d r = 2 π 8 - 1 2

∫ C   F ∙ d r = 16 π - π

Resposta

∫ C   F ∙ d r = 15 π

Exercício Resolvido #6

Diomara Pinto e Maria Cândida Ferreira Morgado, Cálculo Diferencial e Integral de Funções de Várias Variáveis, 3ª ed. Rio de Janeiro: UFRJ, 2009, pp. 294 - 11.

Calcule ∬ S r o t F . n d S , onde F x ,   y ,   z = ( 2 x y ,   0 ,   - x z ) e S é a superfície do elipsoide

x 2 4 + y 2 9 + z 2 16 = 1

Passo 1

Como temos uma superfície fechada e limitada, e F ( x , y , z ) tem sua primeira derivada contínua (classe C 1 ), a integral dada por ∬ S r o t F . n d S tem valor nulo!

Difícil de acreditar, não? Então vamos ver a demostração para confirmar nossa afirmativa.

Passo 2

Primeiro vamos calcular o rotacional do campo F → . Temos que F → = ( 2 x y ,   0 ,   - x z ) e o rotacional pode ser calculado por:

∇ ×   F → = i j k ∂ ∂ x ∂ ∂ y ∂ ∂ z F 1 F 2 F 3

∇ ×   F → = ( 0 ,   z ,   - 2 x )

Passo 3

Vamos parametrizar a superfície! Sua parametrização é semelhante a de uma esfera, para um elipsoide geral da forma:

x 2 a + y 2 b + z 2 c = 1

A parametrização é:

φ θ , ϕ = a c o s θ s e n ϕ ,   b s e n θ s e n ϕ ,   c c o s ϕ

Assim, no nosso caso temos:

φ θ , ϕ = 2 c o s θ s e n ϕ ,   3 s e n θ s e n ϕ ,   4 c o s ϕ

0 ≤ θ ≤ 2 π

0 ≤ ϕ ≤ π

Passo 4

O próximo passo é encontrar a normal,

N → θ , ϕ = ∂ φ ∂ θ × ∂ φ ∂ ϕ

∂ φ ∂ θ = - 2 s e n θ s e n ϕ ,   3 c o s θ s e n ϕ ,   0

∂ φ ∂ ϕ = 2 c o s θ c o s ϕ ,   3 s e n θ c o s ϕ , - 4 s e n ϕ  

N → θ , ϕ =   i j k - 2 s e n θ s e n ϕ 3 c o s θ s e n ϕ 0 2 c o s θ c o s ϕ 3 s e n θ c o s ϕ - 4 s e n ϕ

N → θ , ϕ = ( - 12 s e n 2 ϕ c o s θ ,   - 8 s e n 2 ϕ s e n θ ,   - 6 s e n ϕ c o s ϕ )

Pra tirar esses sinais de menos, vamos considerar a normal voltada pra fora da elipsoide, com isso

N → θ , ϕ = ( 12 s e n 2 ϕ c o s θ ,   8 s e n 2 ϕ s e n θ ,   6 s e n ϕ c o s ϕ )

Você vai ver que não faz diferença se fizer com o sinal de menos, é só pra ficar mais simples mesmo =D

Passo 5

Por último vamos calcular a integral pedida,

∬ S r o t F . n d S

∫ 0 2 π ∫ 0 π 0,4 c o s ϕ , - 4 s e n ϕ c o s θ . 12 s e n 2 ϕ c o s θ ,   8 s e n 2 ϕ s e n θ ,   6 s e n ϕ c o s ϕ d ϕ d θ

∫ 0 2 π ∫ 0 π ( 32 s e n 2 ϕ c o s ϕ s e n θ - 24 s e n 2 ϕ c o s ϕ c o s θ )   d ϕ d θ

∫ 0 2 π 32 c o s θ s e n 3 ϕ 3 0 π - 24 c o s θ s e n 3 ϕ 3 0 π d θ = 0  

Logo, está demonstrado que a integral tem valor nulo!!

Resposta

Ei, a resposta está no passo a passo :)

Exercícios de Livros Relacionados

Uma partícula se move ao longo dos segmentos de reta da origem aos pontos 1,0 , 0 ,1,2 , 1 ( 0,2 , 1 ) e de volta para a origem sob a influência do campo de forças F → = z 2 i → + 2 x y j → + 4 y 4 k
Use o teorema de Stokes para calcular ∬ S r o tF → ⋅ d S . F → x , y , z = x 2 z 2 i → + y 2 z 2 j → + x y z k → S é o hemisfério x 2 + y 2 + z 2 = 16 , y ≥ 0 , orientado em direção do eixo positivo d
Verifique se o Teorema de Stokes é verdadeiro para o campo vetorial dado F → e a superfície S . F → = y i → + z j → + x k → S é o hemisfério x 2 + y ² + z ² = 1 ² ² , y ≥ 0 , orientado na direção posi
Use o teorema de Stokes para calcular ∬ S c u r lF → ⋅ d S . F → x , y , z = e x y c o s c o szi → + x 2 z j → + x y k → , S é o hemisfério x = 1 - y 2 - z 2 orientado na direção positiva do eixo x .
Use o teorema de Stokes para calcular ∫ C F → ⋅ d r → . Em cada caso, C é orientada no sentido anti-horário quando vista de cima. F → x , y , z = y z i → + 2 x z j → + ( e x y ) k → , C é a circunferê