Cálculo de Volumes por Integrais Duplas
Produzido por Arthur Melo de AlmeidaTeoria
Lá no início de tudo eu te motivei a estudar integrais duplas falando que elas representam volumes! Agora vou deixar isso mais claro. Imagina que eu quero o volume entre a função e o plano dentro do retângulo como na figura abaixo:
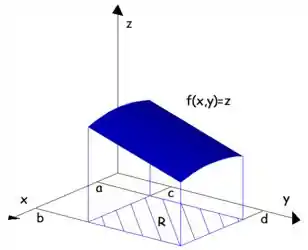
Temos que o volume será dado pela integral dupla, ou seja
ou
(sendo a área de ).
Na prática
Imagina que eu quero calcular volume da região limitada pelos planos , e .
Primeiro, precisamos esboçar a região:
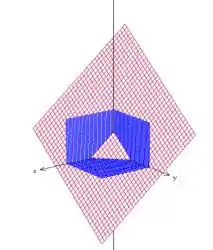
Podemos reescrever o último plano como e pensar que queremos o volume entre a superfície do plano inclinado e a região do plano formada pelo triângulo abaixo:
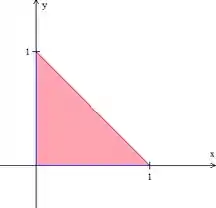
Como esse triângulo foi obtido? Pelo desenho vemos que o domínio é limitado pelos eixos cartesianos e pela interseção do plano com o plano , ou seja, pela reta . Então, representa a “altura” da região em cada ponto e representa a área sobre essa altura. Chamando essa região plana acima de , temos que:
Ou seja, o volume que queremos é a integral da função que representa o plano inclinado na região plana que desenhamos acima.
Então, precisamos escrever matematicamente essa região , como sempre fizemos nas integrais duplas.
Como já mencionado acima, para descobrir a equação da reta inclinada é só fazer a intersecção do plano com , o que nos dá:
Escrevendo a região plana como tipo I, temos que está entre as retas e enquanto está entre e . Portanto, . Levando isso para a integral:
Aí é só resolver!
Ok, vamos ver um exemplo um pouco mais elaborado agora
Calculemos o volume da região limitada pelos paraboloides e .
A região que temos é essa aqui:
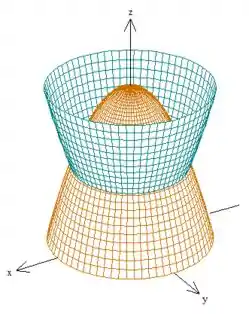
Nós podemos pensar que ela está limitada pelas duas funções e .
A “altura” dessa região, não vai ser sempre ? Ou seja, essa “altura” é!
Bom, se para achar o volume da região, temos que integrar uma altura em uma área, nada mais justo que dizer que:
Onde é a área que limita esse volume no plano (a projeção do volume):
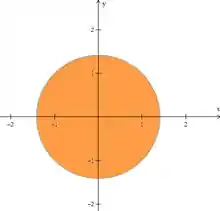
Aí, é só escrever essa região como em qualquer integral dupla que já vimos. Como é um círculo, a boa é usar coordenadas polares.
O círculo fica definido como e .
Esse limite do raio pode ser encontrado fazendo a interseção entre os paraboloides:
Beleza?
Levando isso para a integral, temos:
Aí é só resolver isso aí!
Então, o conceito novo desse capítulo é entender como escrever o volume como uma integral dupla (identificando quem é a “altura” da região e quem é a área que a limita no plano ), depois, a questão é igual a qualquer outra de integral dupla!
Exercícios Resolvidos
Exercício Resolvido #1
James Stewart, Cálculo Vol. 2, tradução da 6ª ed. Norte-americana, Rio de Janeiro: CENGAGE learning, 2010, pp. 916
Calcule o volume do sólido que é delimitado pelo paraboloide elíptico , pelos planos e e pelos planos coordenados.
Passo 1
Para entender o que está sendo pedido, vamos fazer um esboço. Esse seria o paraboloide que o enunciado menciona, vamos primeiro desenhar esse paraboloide:
Repara que a sua equação é
Então o vértice desse paraboloide está no , vai ficar como na figura de baixo.
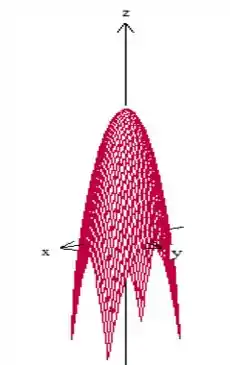
Mas o problema diz que a superfície é cortada pelos planos coordenados ( , e ) e também pelos planos e , certo? Faremos isso. Vamos manter o paraboloide limitado com
O gráfico vai ficar
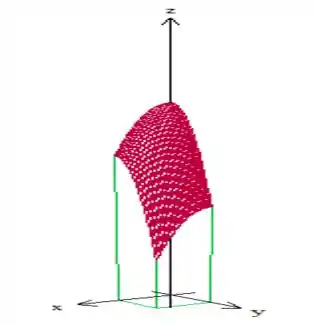
Pronto, é o volume dessa região que a questão pede (uma caixa com a parte de cima curva).
Passo 2
Agora devemos montar o problema em linguagem matemática. Para isso, basta você se lembrar da definição de Integrais Duplas. Integrar uma função em uma região do plano não é equivalente a calcular o volume entre essa superfície e esse plano? Então é isso que faremos.
Vamos escrever a equação do paraboloide em função de e Basta isolar o :
Note que, como os coeficientes de e de ficaram negativos, o paraboloide está virado para baixo. Nunca teremos um valor de maior que (quando e são iguais a zero).
Montaremos, então, a integral:
Passo 3
Para calcularmos essa integral dupla, vamos separá-la em integrais simples:
Devemos, então, encontrar os valores dos limites de integração , , , e . Repare que a região formada no plano ,abaixo do pedaço que restou do paraboloide, é um retângulo que pode ser escrito assim:
Pois tanto como variam entre e . Basta, agora, escrever esses números na integral:
Passo 4
Vamos começar integrando em (a integral de dentro):
Passo 5
Agora, vamos integrar em :
Resposta
Exercício Resolvido #2
PUC-RJ - Cálculo 3 - P1 2013.2 – 3
Seja . Mostre que o volume do sólido limitado pelo plano e pelo paraboloide é igual a:
Sugestão: Use coordenadas polares. Justifique.
Passo 1
Vamos primeiro entender como calcular esse volume. Lembra que o volume que fica embaixo dessa função até o plano vai ser
Onde é aquela região da função onde Vamos descobrir que região é essa
Isso é uma circunferência de centro na origem e raio
Como temos uma circunferência na região vamos usar coordenadas polares.
Passo 2
Faremos então
Passo 3
Falta fazermos o intervalo de integração, como temos um circulo de raio vamos ter
Passo 4
Vamos, então, montar a integral em coordenadas polares:
Passo 5
Vamos começar integrando em relação a :
Passo 6
Integrando, agora, em relação a , temos:
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #3
James Stewart, Cálculo Vol. 2, tradução da 6ª ed. Norte-americana, Rio de Janeiro: CENGAGE learning, 2010, pp. 929
Determine o volume do sólido que está sob o paraboloide , acima do plano e dentro do cilindro .
Passo 1
Calcular o volume entre a função e o plano dentro de uma região é o mesmo que:
Mas que região é essa? Repare que o enunciado limitou a região de integração com um cilindro, que nada mais é que a “repetição” de uma circunferência para qualquer . Portanto, o domínio que buscamos no plano , é limitado por uma circunferência de equação:
Passo 2
Como tanto a função que vamos integrar como a região de integração possuem termos e , vamos utilizar coordenadas polares. Faremos, então:
Passo 3
Agora que já definimos a substituição que faremos, vamos analisar os novos intervalos de integração.
O termo da equação da circunferência indica que ela não está centrada na origem. Vamos, então, completar o quadrado para descobrirmos seu centro:
Portanto, temos uma circunferência de raio centrada em , vamos representá-la graficamente:
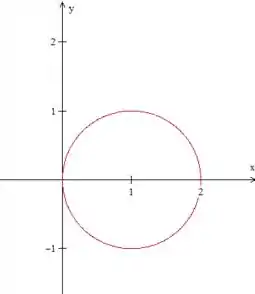
O ângulo varia entre e . Se não ficou claro a partir da imagem, pensa no seguinte: o ângulo deve cobrir toda a parte à direita o eixo , e cresce no sentido anti-horário, certo? Então, a partir da origem, o ângulo deve começar cobrindo a parte de baixo da curva, e seu valor inicial é . No ponto , vamos ter . Quando a curva começa a ser fechada na origem, vai se aproximando do valor .
Já , varia entre e a curva em vermelho, então, vamos substituir os valores que definimos para e na expressão do círculo:
Como sempre, teremos:
Passo 4
Vamos, então, montar a integral em coordenadas polares:
Passo 5
Vamos começar integrando em relação a :
Passo 6
Para integrar em relação a , vamos utilizar a fórmula do arco duplo:
Aplicando essa fórmula novamente:
Resposta
Exercício Resolvido #4
UERJ - Cálculo 2 - Selecionados Lista 21 - 4a
Calcule o volume do sólido delimitado pelo gráfico de:
Passo 1
Bom, antes de mais nada, vamos desenhar essa região do problema, para visualizar melhor as coisas.
Nós temos o plano , o plano e o , que são traquilos de desenhar. Agora vamos pensar no .
Você pode fazer a reta no plano , tendo em mente que ela corta o eixo em (é o ponto onde ) e que cresce quando cresce, não precisa ser nada perfeito não! É um esboço. Agora, a equação do plano não possui a coordenada , basta “repetirmos” essa reta ao longo do eixo .
Agora vamos ao último plano . Repara que ele não tem a coordenada , então, basta desenharmos a reta no plano e repetí-la ao longo do eixo .
Temos então a seguinte região:
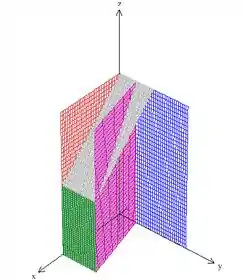
Aqui vai um outro ponto de vista, se você ficou confuso:
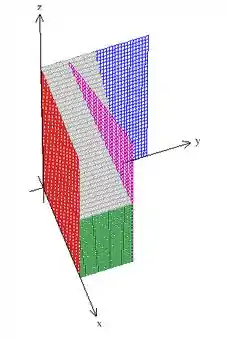
Beleza? Como o problema não menciona nenhum plano fechando a região por baixo, vamos assumir que , ou seja, que o volume é limitado pelo plano . Agora, chamando de essa região que acabamos de analisar, o problema pede então .
Passo 2
Certo, agora precisamos escrever matematicamente essa região, ok? Podemos ver que, na coordenada ela é limitada por duas funções ( e ) e no plano , por uma área, que chamaremos de .
Sendo assim, esse volume pode ser escrito da seguinte forma:
Passo 3
Agora precisamos escrever matematicamente essa área , como em qualquer integral dupla que já fizemos. Imagine o sólido visto de cima, temos isso aqui:
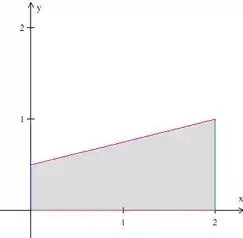
Essa é a área que limita no plano . Vamos descrevê-la como uma região do tipo I, na coordenada ela é limitada por funções (a reta vermelha e a roxa ) e na coordenada é limitada por números ( e ).
Podemos então escrever o seguinte:
Passo 4
Agora vamos substituir na integral esses intervalos que encontramos:
Cuidado com a ordem dos diferenciais! Ela tem que acompanhar os intervalos da integrais.
Passo 5
Agora em relação a :
Passo 6
Finalmente, integramos em relação a :
Resposta
Exercício Resolvido #5
UERJ - Cálculo 2 - Selecionados Lista 21 - 4b
Calcule o volume do sólido delimitado pelo gráfico de:
Passo 1
Antes de tudo, vamos desenhar essa região para entender melhor o problema. Temos um plano , um cilindro de base parabólica e um plano .
Para o cilindro, é uma boa você desenhar a parábola no plano e depois repeti-la ao longo do eixo (afinal, a coordenada não está presente na equação, o que significa que ela vale para qualquer ). Para o plano , fazemos o mesmo, desenhamos a reta no plano e a repetimos ao longo do eixo . O outro plano, , já é mais chatinho de desenhar, mas como isso aqui é só um esboço, você pode desenhar um plano qualquer, é só para termos uma noção da região mesmo.
No plano , a região é limitada pelo cilindro e pelo plano verde e na coordenada , limitada pelo plano azul. Como não há mais informações para limitar a coordenada , vamos assumir que , para continuarmos o problema.
Nossa região é então a que está entre as superfícies vermelha e verde e abaixo do plano azul:
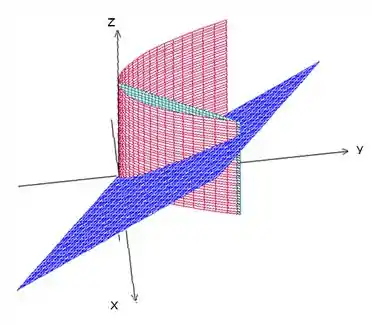
Chamando de essa região que acabamos de analisar, o problema pede então .
Passo 2
Beleza, agora precisamos escrever matematicamente essa região. Como podemos ver, na coordenada ela está limitada pela equação do plano azul e pelo plano , enquanto no plano ela é limitada pela seguinte àrea:
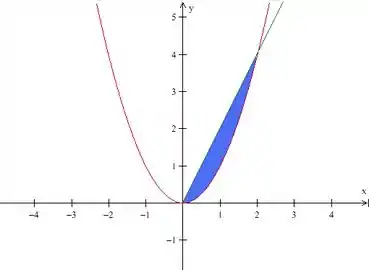
Essa seria a região vista de cima, percebeu? O plano verde virou uma reta e o cilindro de parábola virou uma parábola . Certo, então vamos escrever o seguinte:
Onde é essa área que acabamos de ver acima.
Passo 3
Agora precisamos escrever matematicamente essa área, como em qualquer integral dupla que já fizemos.
Vamos enxergar essa área como região do tipo I, limitada na coordenada por funções (a equação da parábola e da reta) e em por números.
Como em a área está entre a equação da parábola e a da reta, temos que:
Agora vamos ver a coordenada . Pela figura, vemos que varia desde a origem até o encontro da reta com a parábola, que acontece em (para ver isso, basta substituir uma equação na outra). Então temos:
Beleza, então vamos escrever essa área assim:
Passo 4
Agora vamos substituir na integral esses intervalos que encontramos:
Cuidado com a ordem dos diferenciais! Ela tem que acompanhar os intervalos da integrais.
Passo 5
Agora em relação a :
Passo 6
Finalmente, em relação a :
Resposta
Exercício Resolvido #6
UERJ - Cálculo 2 - Selecionados Lista 21 - 4c
Calcule o volume do sólido delimitado pelo gráfico de:
Passo 1
Bom, antes de mais nada, vamos desenhar essa região do enunciado.
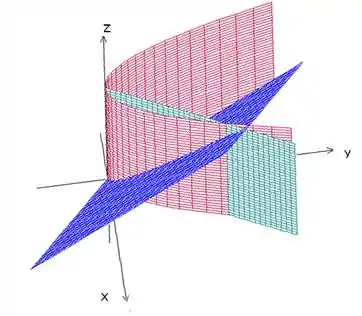
Obs: Tem uma superfície de equação meio esquisita aí, não é?
Não é necessário para essa questão que você saiba que superfície é essa, mas, a título de curiosidade, vamos mostrar aqui. Essa é uma cela, oblíqua aos eixos coordenados e :
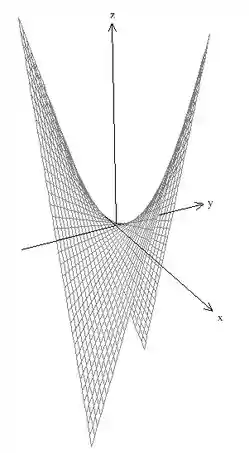
Se você não soubesse disso na questão não tinha problema nenhum, basta você entender que essa superfície limita a região “por cima” dela, já que é a única equação do enunciado em que a coordenada está presente. Bom, vamos lá.
Nós temos a superfície , que já vimos. Temos também , basta desenhar a reta no plano e alongar pelo eixo , formando um plano. Fazemos o mesmo para os planos e .
Temos então a seguinte região:
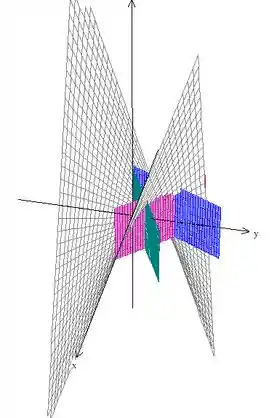
Outro ângulo, para você visualizar melhor:
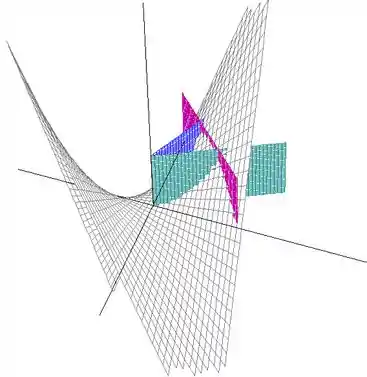
Beleza? Como o problema não menciona nenhum plano fechando a região por baixo, vamos assumir que , ou seja, que o volume é limitado pelo plano . Agora, chamando de essa região que acabamos de analisar, o problema pede então .
Passo 2
Certo, agora precisamos escrever matematicamente essa região, ok? Vemos que, na coordenada ela é limitada por duas funções ( e ) e no plano , por uma área, que chamaremos de .
Sendo assim, esse volume pode ser escrito da seguinte forma:
Passo 3
Agora precisamos escrever matematicamente essa área , como em qualquer integral dupla que já fizemos. Imagine o sólido visto de cima, temos isso aqui:
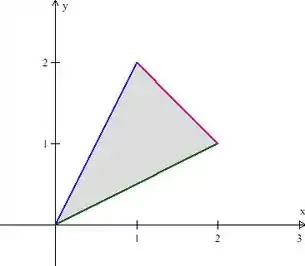
Essa é a área que limita no plano . Vamos descrevê-la como uma região do tipo I, na coordenada ela é limitada por funções e na coordenada é limitada por números. Aqui não tem jeito, precisamos dividir essa região em duas, a da esquerda com e a da direita com . Vamos chamá-las de e , .
A região da esquerda é limitada na coordenada pela reta verde e pela azul , enquanto a da esquerda é limitada pela reta roxa e pela verde .
Podemos então escrever o seguinte:
Passo 4
Agora vamos substituir na integral esses intervalos que encontramos:
Cuidado com a ordem dos diferenciais! Ela tem que acompanhar os intervalos da integrais.
Passo 5
Agora em relação a :
Passo 6
Finalmente, em relação a :