Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Mudança Qualquer de Variáveis

Ver Todos os Exercícios

Teoria

Introdução

Olá! Como estamos estudando integrais duplas, eu vou lançar um desafio: calcular a expressão abaixo.

∬ D   x + 2 y sen ⁡ x - 2 y d x d y

Onde D = 0,3 × 0,1 .

Opa, essa integral parecer sem complicadinha, né? Nem sempre as integrais são simples para resolvermos diretamente, às vezes precisamos “mexer” um pouco nelas.

Não seria muito mais simples se fosse assim? ∬ D   u sen ⁡ ( v ) d u d v

Então, chegamos ao objetivo do nosso capítulo! Aprender como mudar as variáveis das integrais, procurando deixá-las mais fáceis de calcular.

Então vamos resolver esse exemplo ai!

Passo 1: Para escrevermos da forma mais simples o primeiro é fazer a substituição. Neste caso definimos que:

u = x + 2 y v = x - 2 y

Daí, a gente pode somar as duas equações e achar uma equação para x :

u + v = x + 2 y + x - 2 y

2 x = u + v

x = u 2 + v 2

Agora, se a gente substitui esse valor de x na equação para u :

u = u 2 + v 2 + 2 y

Assim, conseguimos uma equação para y :

2 y = u 2 - v 2

y = u 4 - v 4

Opa, então nossas expressões são:

x = u 2 + v 2

y = u 4 - v 4

Beleza?

Passo 2: Sempre que fizermos uma mudança de variável não podemos esquecer de calcular o Jacobiano, que é feito desse jeitinho aqui:

J = ∂ ( x , y ) ∂ ( u , v ) = ∂ x ∂ u ∂ x ∂ v ∂ y ∂ u ∂ y ∂ v

Nunca, de forma alguma, se esqueça de inserir o Jacobiano quando você trocar as variáveis! Se você esquecer, já vai começar a questão com a integral errada.

Como nós mudamos as variáveis para u e v , nós precisamos de um termo faz a relação entre os diferenciais. Esse termo é o Jacobiano, ok. E quando fazemos isso, estamos usando o Teorema da mudança de variáveis.

Um fato interessante do jacobiano é que ele nunca pode ser 0. Caso você encontre 0, refaça as contas ou faça uma nova mudança de variável.

No caso do nosso exemplo ficamos com:

∂ x ∂ u = 1 2 ∂ x ∂ v = 1 2 ∂ y ∂ u = 1 4 ∂ y ∂ v = - 1 4

J = 1 2 1 2 1 4 - 1 4 = - 1 4

Passo 3: Agora nós temos que substituir tudo na nossa nova integral que tem essa cara

∬ D   f u , v . J d u d v

Percebe que o que a gente multiplica na integral quando fazemos uma mudança é o módulo do Jacobiano. ∬ D   u s e n v - 1 4 d u d v

Podemos colocar essa constante para fora e a nossa integral fica assim:

1 4 ∬ D   u s e n v d u d v

Passo 4: A última coisinha que temos que prestar atenção são os novos limites de integração!

u = x + 2 y v = x - 2 y

Só que como os limites de x são [ 0 x 3 ] e y [ 0 x 1 ] , vamos substituir os valores para achar os novos limites de u e v .

Substituindo, temos que os limites de u são [ 0 x 5 ] e os limites de v são [ 0 x 1 ]

Então nossa integral final fica:

1 4 ∫ 0 1   ∫ 0 5 u s e n v d u d v

1 4 ∫ 0 1   u 2 2 s e n v [ 0 5 d v =   1 4 ∫ 0 1   5 2 2 s e n v d v =   25 8 ∫ 0 1   s e n v d v

25 8 ∫ 0 1   s e n v d v = 25 8 - c o s v [ 0 1 d v = 25 8 ( 1 - cos ⁡ 1 )

Agora que ficou mais tranquilinho de entender pelo exemplo vamos ver como se faz de forma genérica!

Lembra que você tinha que calcular a relação entre os diferenciais e os novos limites de integração? Por exemplo, se fazemos x 2 = u , teremos que 2 x   d x = d u . Se os limites iniciais fossem x = a e x = b eles passarão a ser u = a 2 e u = b 2 . Esse método se baseia na seguinte fórmula:

∫ f g x ⋅ g ' x d x = ∫ f u d u

Vamos fazer o equivalente para as integrais duplas, pois não podemos simplesmente trocar as variáveis sem compensar a integral e a região de integração. Vamos transformar uma integral do tipo

∬ D   f x , y   d x d y

Transformando f x , y em h u , v , nós ficamos com

∬ Q   h u , v   | J | d u d v

Dica: Algumas vezes você vai fazer substituições em que é complicado isolar o x e o y para calcular as derivadas parciais, por exemplo, x 3 + y = u e v = x y . Nesses casos, tem um jeito mais simples para calcular o Jacobiano.

Se queremos ∂ ( x , y ) ∂ ( u , v ) = J , podemos calcular ∂ ( u , v ) ∂ ( x , y ) = J * , usando as derivadas parciais de u e v e inverter esse resultado. Pois:

J = 1 J *

Vamos ver isso melhor nos exercícios!

Mudança linear de variáveis

Galera, agora vou falar com vocês sobre uma forma especial de substituir variáveis em integrais duplas. Essa forma é quando fazemos uma transformação linear. Considere uma transformação linear T definida assim:

x = a u + b v   y = c u + d v

(Sendo a , b , c e d constantes)

O determinante Jacobiano será dado por

J = ∂ ( x , y ) ∂ ( u , v ) = a b c d = a d - b c

Portanto, quando tivermos uma mudança linear de variáveis, o Jacobiano dessa transformação será sempre um número.

Exemplo: Calcule

∬ D   e y - x y + x     d x d y

Onde D é a região triangular limitada pela reta y + x = 2 e os eixos coordenados.

Passo 1: Observando a integral, vemos que o expoente y - x y + x não é uma expressão muito simples. Então, vamos tentar simplificá-la por meio de substituições. Não seria muito melhor se tivéssemos apenas e u v ? É o que faremos, para isso, vamos definir:

u = y - x e v = y + x

Somando as expressões teremos

u + v = 2 y

Subtraindo as expressões teremos

v - u = 2 x

Portanto:

x = v - u 2 y = u + v 2

Passo 2: Pronto, já escolhemos nossa substituição, agora vamos calcular o seu Jacobiano.

Temos:

∂ x ∂ u = - 1 2

∂ y ∂ v = 1 2

∂ x ∂ v = 1 2

∂ y ∂ u = 1 2

J = ∂ ( x , y ) ∂ ( u , v ) = - 1 2 1 2 1 2 1 2 = - 1 2 1 2 - 1 2 1 2 = - 1 2

J = 1 2

Passo 3: Agora vamos calcular os novos intervalos. Antes tínhamos y + x = 2 e os eixos coordenados x = 0 e y = 0 limitando nossa região de integração, vamos substituir as novas variáveis nessas expressões:

x = 0   →   v - u 2 = 0   → u = v

y = 0   →   u + v 2 = 0   → u = - v  

y + x = 2   →   v - u 2 +   u + v 2 = 2   → v = 2

No plano u v , essas expressões definem a seguinte região:

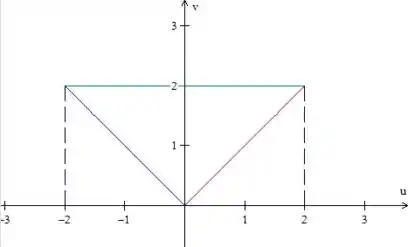
Passo 4: Vamos, agora, escrever esse domínio como tipo II (à esquerda e à direita temos funções e em cima e embaixo temos números). Como podemos ver, v varia de 0 a 2 , portanto:

0 ≤ v ≤ 2

A variável u está entre a reta azul - v = u e a vermelha v = u , assim temos:

- v ≤ u ≤ v

Passo 5: A integral passa a ser, então:

∫ 0 2   ∫ - v v e u v 1 2 d u d v =

= 1 2 ∫ 0 2 v e u v u = - v u = v d v =

= 1 2 ∫ 0 2 v e v v - e - v v d v =

= 1 2 ∫ 0 2 v e - 1 e d v =

= v 2 4 e - 1 e 0 2 =

= e - 1 e

Beleza, vamos ver isso melhor nos exercícios agora!

Mudança linear de variáveis

Exercícios Resolvidos

Exercício Resolvido #1

Diomara Pinto e Maria Cândida Ferreira Morgado, Cálculo Diferencial e Integral de Funções de Várias Variáveis, 3ª ed. Rio de Janeiro: UFRJ, 2009, pp. 185, adaptado.

Considere a aplicação g definida por:

x = u + v

y = v - u 2

Utilizando g , calcule ∬ D   x - y + 1 4 - 1 2 d x d y , onde D é a imagem no plano x y da região Q no plano u v limitada pelas retas u = 0 , v = 0 e u + v = 2 .

Passo 1

Como o enunciado já disse as substituições que devemos fazer, precisamos agora calcular o Jacobiano dessa transformação. Já temos x e y escritos em função de u e v , não é?

x = u + v

y = v - u 2

Temos J = ∂ ( x , y ) ∂ ( u , v )     = ∂ x ∂ u ∂ x ∂ v ∂ y ∂ u ∂ y ∂ v

∂ x ∂ u = 1

∂ x ∂ v = 1

∂ y ∂ u = - 2 u

∂ y ∂ v = 1

J = 1 1 - 2 u 1 = 1 1 - 1 - 2 u = 1 + 2 u

Passo 2

Sabemos que, no plano x y , a região de integração é dada por D , como está na integral do problema. Passando as coordenadas para u e v , a região passa a ser Q , como o próprio enunciado diz. Agora vamos fazer as substituições na integral:

∬ Q     u + v - v - u 2 + 1 4 - 1 2 ⋅ ( 1 + 2 u ) d u d v =

= ∬ Q   u + u 2 + 1 4 - 1 2 ⋅ ( 1 + 2 u ) d u d v =

= ∬ Q   u + 1 2 2 - 1 2 ⋅ ( 1 + 2 u ) d u d v =

= ∬ Q   u + 1 2 - 1 ⋅ ( 1 + 2 u ) d u d v =

= ∬ Q   2 u + 1 2 - 1 ⋅ ( 1 + 2 u ) d u d v =

= ∬ Q   2 2 u + 1 ⋅ 1 + 2 u d u d v =

∬ Q   2   d u d v

Passo 3

Agora precisamos descrever essa região Q , limitada por u = 0 , v = 0 e u + v = 2 no plano u v . Vamos fazer um esboço.

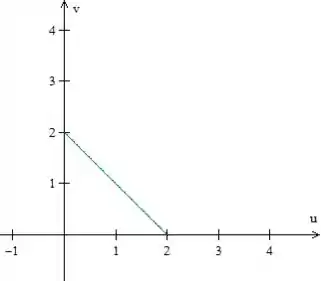
Podemos descrevê-la como região do tipo I, com 0 ≤ u ≤ 2 e 0 ≤ v ≤ 2 - u . A integral iterada será:

∫ 0 2 ∫ 0 2 - u 2   d v d u =

Passo 4

Integrando em relação a v , temos:

= ∫ 0 2 2 v v = 0 v = 2 - u d u =

= ∫ 0 2 2 2 - u d u =

= ∫ 0 2 4 - 2 u   d u =

Passo 5

Integrando, agora, em relação a u :

= 4 u - u 2 0 2 =

= 8 - 4 =

Resposta

4

Exercício Resolvido #2

Diomara Pinto e Maria Cândida Ferreira Morgado, Cálculo Diferencial e Integral de Funções de Várias Variáveis, 3ª ed. Rio de Janeiro: UFRJ, 2009, pp. 185, adaptado.

Calcule ∬ D   y + 2 x y - 2 x - 1 d x   d y onde D é a região do plano x y limitada pelas retas y - 2 x = 2 , y + 2 x = 2 , y - 2 x = 1 e y + 2 x = 1 .

Passo 1

Como temos os termos ( y + 2 x ) e ( y - 2 x ) tanto na integral quanto nos limites da região, vamos fazer a seguinte substituição:

u = y + 2 x

v = y - 2 x

O que podemos reescrever como y = u + v 2 e x = u - v 4 .

Passo 2

Temos J = ∂ ( x , y ) ∂ ( u , v )     = ∂ x ∂ u ∂ x ∂ v ∂ y ∂ u ∂ y ∂ v

∂ x ∂ u = 1 4

∂ x ∂ v = - 1 4

∂ y ∂ u = 1 2

∂ y ∂ v = 1 2

J = 1 4 - 1 4 1 2 1 2 = 1 8 + 1 8 = 1 4

Fazendo a substituição na integral, temos, então:

1 4 ∬ D *   u v - 1 d u   d v

Passo 3

Vamos, agora, analisar a nova região de integração, teremos:

y - 2 x = 2   → v = 2

y + 2 x = 2   → u = 2

y - 2 x = 1   → v = 1

y + 2 x = 1   → u = 1

Assim, a integral iterada passa a ser:

1 4 ∫ 1 2 ∫ 1 2 u v - 1 d u   d v =

Passo 4

Integrando em relação a u , temos:

= 1 8 ∫ 1 2 u 2 v - 1 u = 1 u = 2 d v =

= 3 8 ∫ 1 2 1 v - 1 d v =

Passo 5

Para concluir a integração, vamos chamar v - 1 = k , d v = d k . Nessa variável, os limites ficam:

v = 1 → k = 1 - 1 = 0

v = 2 → k = 2 - 1 = 1

Então, a gente pode reescrever a integral como:

= 3 8 ∫ 0 1 k - 1 2 d k =

= 3 8 ⋅ 2 k 1 2 0 1 =

= 3 4 ( 1 - 0 ) =

Resposta

3 4

Exercício Resolvido #3

UFRJ, Cálculo III, P1/2013.2, 1

Seja D = { ( x , y ) ∈ R 2 ; x + y ≥ 0 ,   y ≤ 0 ,   x ≤ 1 } . Calcular o valor da integral

∬ D   x 3 x + y d A

Passo 1

Essa expressão parece complicada tanto para integrar em x quanto em y , pois o termo dentro da raiz quadrada não é muito simples. Vamos, então, procurar uma substituição que facilite essa integração. Faremos:

u = x e v = x + y

Assim, o radicando passa a ser simplesmente v .

Passo 2

Agora vamos calcular o Jacobiano dessa transformação.

Escrevendo as equações de x e de y em função das novas variáveis u e v , temos o sistema:

x = u v = u + y   → y = v - u

Temos, então>

∂ x ∂ u = 1

∂ y ∂ v = 1

∂ x ∂ v = 0

∂ y ∂ u = - 1  

J = ∂ ( x , y ) ∂ ( u , v ) = 1 0 - 1 1 = 1

Passo 3

Agora vamos calcular os novos intervalos. Como a região de integração fica mais complexa nas variáveis u e v , vamos fazer o gráfico no plano x y :

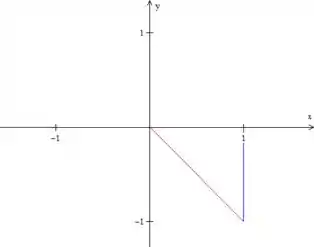
Assim, fica mais fácil ver que 0 ≤ x ≤ 1 e - x ≤ y ≤ 0 , pois a reta vermelha é y = - x . Precisamos, agora, “traduzir” esses limites para as novas variáveis, substituindo os valores que atribuímos a x e a y . Primeiro o limite em x :

0 ≤ x ≤ 1   → 0 ≤ u ≤ 1

Agora, o limite em y fica:

- x ≤ y ≤ 0   → - u ≤ v - u ≤ 0

0 ≤ v ≤ u

Passo 4

Agora vamos montar a nova integral em termos de u e v :

∫ 0 1   ∫ 0 u u 3   v 1 2 d v d u =

Passo 5

Integraremos, então, em relação a v :

= ∫ 0 1 2 3 u 3 v 3 2 v = 0 v = u d u =

= 2 3 ∫ 0 1 u 3 u 3 2 d u = 2 3 ∫ 0 1 u 9 2 d u =

Passo 6

Integraremos, então, em relação a u :

= 2 3 × 2 11 u 11 2 0 1 d u =

Resposta

4 33

Exercício Resolvido #4

Diomara Pinto e Maria Cândida Ferreira Morgado, Cálculo Diferencial e Integral de Funções de Várias Variáveis, 3ª ed. Rio de Janeiro: UFRJ, 2009, pp. 185, adaptado.

Calcule ∬ D   ( 2 x + 1 ) d x d y onde D é a região do primeiro quadrante do plano x y , limitada pelas curvas y = x 2 , y = x 2 + 1 , x + y = 1 e x + y = 2 .

Passo 1

Como temos os termos ( y - x 2 ) e ( x + y ) mais de uma vez nas equações que limitam a região de integração, vamos fazer a seguinte substituição:

u = y - x 2

v = x + y

Passo 2

Agora vamos calcular o Jacobiano dessa transformação.

Nesse caso, escrever as equações de x e de y em função das novas variáveis u e v não é muito simples. Por isso, vamos usar um recurso para facilitar nossa vida, em vez de calcular ∂ ( x , y ) ∂ ( u , v ) = J , vamos calcular ∂ ( u , v ) ∂ ( x , y ) = J * (que é o inverso do Jacobiano que queremos).

J * = ∂ u ∂ x ∂ u ∂ y ∂ v ∂ x ∂ v ∂ y

Temos, então:

∂ u ∂ x = - 2 x

∂ u ∂ y = 1

∂ v ∂ x = 1

∂ v ∂ y = 1

J * = - 2 x 1 1 1 = - 2 x 1 - 1 1 = - 2 x - 1 = - ( 2 x + 1 )

Esse valor que encontramos ainda não é o Jacobiano:

J = 1 | J * | = 1 2 x + 1

Deveríamos, agora, escrever esse Jacobiano em função de u e v , as nossas novas variáveis. Porém, isso seria trabalho desnecessário, repare que essa expressão é o inverso do que temos na nossa integral.

Digamos que escrevemos | J | em função de u e v e encontramos uma expressão F ( u , v ) , teremos:

∬ D *   F ( u , v ) × 1 F u , v   d u d v

Como o termo ( 2 x + 1 ) também está na integral, eles se cancelam! A integral passa a ser então:

∬ D *     d u d v

Passo 3

Agora precisamos descobrir os intervalos de integração no domínio D * . Lembrando da definição das variáveis:

y = x 2   → u = x 2 - x 2 = 0

y = x 2 + 1   → u = x 2 + 1 - x 2 = 1

x + y = 1   → v = 1

x + y = 2   → v = 2

Muito mais simples, não é? A integral iterada será então:

∫ 1 2 ∫ 0 1 d u d v =

Passo 4

Integrando em relação a u , temos:

∫ 1 2 u u = 0 u = 1 d v =

∫ 1 2 d v =

Passo 5

Integrando, agora, em relação a v :

= v 1 2 =

Resposta

1

Exercício Resolvido #5

UFRJ - Cálculo 3 - P1 2010.2 – 1

Calcule a integral dupla ∬ D   2 x + y s e n ( x - 2 y ) d x d y , onde D é a região delimitada pelas curvas dadas pelas equações   2 x + y 2 - 2 y + x = - 3 , 2 x + y 2 - 2 y + x = 0 , 2 x + y = 1 e 2 x + y = 0 .

Passo 1

Essa integral, não parece muito simples de se calcular. Analisando o domínio, não conseguimos identificar de primeira que região é essa, para escrevermos como tipo I ou II. Por isso, precisamos fazer substituições.

Repare que os termos 2 x + y e x - 2 y aparecem tanto na integral como nas curvas que limitam a região de integração, isso nos leva a pensar que talvez seja uma boa substituí-los por outra variável. É que faremos, vamos definir:

2 x + y = u e x - 2 y = v

Passo 2

Agora vamos calcular o Jacobiano dessa transformação.

Escrevendo as equações de x e de y em função das novas variáveis u e v , temos o sistema:

y + 4 y = u - 2 v   → y = u - 2 v 5 4 x + x = 2 u + v   → x = 2 u + v 5 .

Temos, então>

∂ x ∂ u = 2 5

∂ y ∂ v = - 2 5

∂ x ∂ v = 1 5

∂ y ∂ u = 1 5

J = ∂ ( x , y ) ∂ ( u , v ) = 2 5 1 5 1 5 - 2 5 = 2 5 - 2 5 - 1 5 1 5 = - 4 - 1 25 = - 1 5

J = 1 5

Você também poderia ter calculado ∂ ( u , v ) ∂ ( x , y ) e invertido o resultado

Passo 3

Agora vamos calcular os novos intervalos, substituindo u e v as equações das curvas do enunciado:

2 x + y = 1   → u = 1

2 x + y = 0   → u = 0

2 x + y 2 - 2 y + x = - 3   →   u 2 + v = - 3

2 x + y 2 - 2 y + x = 0   → u 2 + v = 0

Nos planos u v , essas expressões definem a seguinte região:

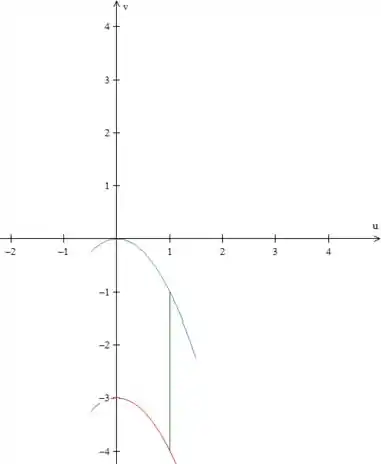
A curva vermelha e a azul são parábolas viradas para baixo.

Passo 4

Vamos, agora, escrever esse domínio como tipo I (em cima e embaixo temos funções e à esquerda e à direita demos números). Como podemos ver, u varia de 0 a 1 , portanto:

0 ≤ u ≤ 1

A variável v está entre a curva vermelha v = - 3 - u 2 e azul v = - u 2 , assim temos:

- 3 - u 2 ≤ v ≤ - u 2

Passo 5

Agora vamos montar a nova integral, substituindo os valores de u e v :

∫ 0 1   ∫ - 3 - u 2 - u 2 u   s e n   v   1 5 d v d u =

Passo 6

Integraremos, então, em relação a v :

= 1 5 ∫ 0 1 - cos ⁡ v   u v = - 3 - u 2 v = - u 2 d u =

= - 1 5 ∫ 0 1 u ( cos ⁡ ( - u 2 ) - cos ⁡ ( - 3 - u 2 ) )   d u =

Passo 7

Para terminar a integração, faremos a substituição u 2 = k , temos

2 u d u = d k → u d u = d k 2

Assim, conseguimos “eliminar” esse termo u que multiplica os cossenos. Vamos reorganizar aqui nossa integral:

- 1 5 ∫ 0 1 ( cos ⁡ ( - u 2 ⏟ - k ) - cos ⁡ ( - 3 - u 2 ⏟ - 3 - k ) ) u d u ⏟ d k / 2 =

Passando o sinal de menos pra dentro, invertemos a ordem da subtração

= 1 5 ∫ 0 1 cos ⁡ - 3 - k - cos ⁡ - k d k 2 =

= 1 5 . 1 2 ∫ 0 1 ( cos ⁡ - 3 - k - cos ⁡ - k ) d k =

= 1 10 ∫ 0 1 ( cos ⁡ - 3 - k - cos ⁡ ( - k ) )   d k =

= 1 10 ( - s e n - 3 - k + s e n - k ) k = 0 k = 1 =

= 1 10 ( s e n 3 + k - s e n k ) k = 0 k = 1 =

= 1 10 ( s e n 4 - s e n 1 - ( s e n   3 - s e n 0 ) =

Resposta

= 1 10 [ s e n   4 - s e n   1 - s e n   3 ]

Exercício Resolvido #6

UNICAMP - Cálculo 2 - P2 2013 Manhã – 4

Calcule

∫ ∫ R   y - 2 x 3 y + 2 x d A

Onde R é o paralelogramo de vértices ( 1,2 ) , ( 2,4 ) , ( 5,2 ) e ( 4,0 ) .

Sugestão: faça uma mudança de variáveis conveniente.

Passo 1

Antes de tudo, vamos fazer um esboço da região para entender melhor o que está sendo pedido.

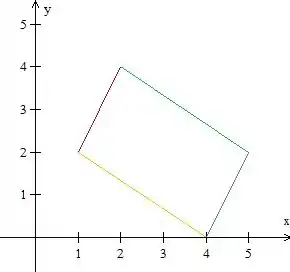
Esse é o paralelogramo da questão. Bom, vamos começar encontrando as equações dessas retas que limitam nossa região. Sabendo que a equação geral da reta y = a x + b , vamos substituir os pontos que definem cada um desses segmentos para encontrar as equações.

Para o segmento vermelho

Substituindo os pontos ( 1,2 ) e ( 2,4 ) , temos:

2 = a + b 4 = 2 a + b

a = 2

b = 0

Temos portanto a equação

y = 2 x

Para o segmento verde

Substituindo os pontos ( 2,4 ) e ( 5,2 ) , temos:

4 = 2 a + b 2 = 5 a + b

a = - 2 3

b = 16 3

Temos portanto a equação

y = - 2 x 3 + 16 3

Para o segmento azul

Substituindo os pontos ( 5,2 ) e ( 4,0 ) , temos:

2 = 5 a + b 0 = 4 a + b

a = 2

b = - 8

Temos portanto a equação

y = 2 x - 8

Para o segmento amarelo

Substituindo os pontos ( 1,2 ) e ( 4,0 ) , temos:

2 = a + b 0 = 4 a + b

a = - 2 3

b = 8 3

Temos portanto a equação

y = - 2 x 3 + 8 3

Passo 2

Ok, e agora? Percebeu que escrever essa região tanto como tipo I ou II vai dar um trabalhinho, não é? Vamos pensar um pouco, repara nas equações das retas que encontramos:

y = 2 x

y = - 2 x 3 + 16 3

y = 2 x - 8

y = - 2 x 3 + 8 3

Já deu para ver alguma semelhança aí, né? Vamos reescrever essas equações:

y - 2 x = 0

y + 2 x 3 = 16 3

y - 2 x = - 8

y + 2 x 3 = 8 3

Vamos agora chamar:

y - 2 x = u

y + 2 x 3 = v

Calma, você já vai entender o porquê disso! Aplicando nas equações, temos:

u = 0

v = 16 3

u = - 8

v = 8 3

Com essa mudança de variáveis, essas são as equações que passam a limitar nossa região, bem mais bonito, não é? O que nós fizemos, basicamente, foi transformar o nosso paralelogramo do plano x y em um retângulo bonitinho no plano u v . Por isso que os intervalos passaram a ser números.

Bom, no plano u v podemos então descrever a região como

D = x , y - 8 ≤ u ≤ 0 ; 8 3 ≤ v ≤ 16 3

Passo 3

Bom, mas como tudo na vida tem um preço, não poderia ser tão simples assim né.

Temos que calcular o Jacobiano dessa transformação, lembra?

J = ∂ ( x , y ) ∂ ( u , v ) = ∂ x ∂ u ∂ x ∂ v ∂ y ∂ u ∂ y ∂ v

Temos:

y - 2 x = u

y + 2 x 3 = v

Isso nos dá

x = 3 8 ( v - u )

y = 3 v 4 + u 4

∂ x ∂ u = - 3 8

∂ x ∂ v = 3 8

∂ y ∂ u = 1 4

∂ y ∂ v = 3 4

J = - 3 8 3 8 1 4 3 4 = - 3 8 3 4 - 1 4 × 3 8   = - 12 32 = - 3 8

Passo 4

Beleza, agora vamos montar a integral:

∫ ∫ R   y - 2 x 3 y + 2 x d A

Nas novas variáveis

y - 2 x = u

y + 2 x 3 = v

Temos, então

= 3 8 ∫ ∫ R *   u 3 v d A =

Show? Lembrando que temos que levar para a integral o módulo do Jacobiano.

Aplicando os intervalos que encontramos:

= 1 8 ∫ 8 3 16 3 ∫ - 8 0 u v   d u d v =

Passo 5

Agora é só resolver isso aí

= 1 16 ∫ 8 3 16 3 u 2 v - 8 0 d v =

= - 1 16 ∫ 8 3 16 3 64 v d v =

= - 4 ∫ 8 3 16 3 1 v d v =

= - 4 ln ⁡ v 8 / 3 16 / 3 =

= - 4 ln ⁡ 16 3 - ln ⁡ 8 3 =

= - 4 ln ⁡ 16 8

= - 4 ln ⁡ 2

Resposta

- 4 ln ⁡ 2

Exercícios de Livros Relacionados

Determine o jacobiano da transformação.x = v + w^2 , y = w + u^2 , z = u + v^2
Calcule a integral, efetuando uma mudança de variáveis apropriada. ∫ ∫ R x - 2 y 3 x - yd A , onde R é o paralelogramo delimitado pelas retas x - 2 y = 0, x - 2 y = 4, 3 x - y = 1, 3 x - y = 8
Utilize a transformação dada para calcular a integral. ∬ R 4 x + 8 y d A , onde R é o paralelogramo com vértices - 1,3 , 1 , - 3 , 3 , - 1 e 1,5 ; x = 1 4 u + v , y = 1 4 v - 3 u
Calcule ∫ ∫ D y + 2 x y - 2 x - 1 d x d y , onde D é a região do plano x y limitada por y - 2 x = 2 , y + 2 x = 2 , y - 2 x = 1 e y + 2 x = 1 .
Calcule ∫ ∫ D xd x d y , onde D é a região do plano x y limitada pelas parabolas x = y 2 - 1 , x = 1 - y 2 e x = 4 - y 2 4 .