Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Mudança para coordenadas polares

Ver Todos os Exercícios

Teoria

E aí?! Você chegou no Responde Aí! E agora vamos entender como efetuar mudança para coordenadas polares.

Mudanças para coordenadas polares são muito importantes, pois muitos problemas são mais fáceis de resolver usando coordenadas polares ao invés de cartesianas.

Para executar uma mudança para coordenadas polares a gente precisa ter na cabeça a seguinte relação:

  1. A gente usa a relação acima para transformar em uma :
  2. Usamos novamente a relação acima para determinar os novos extremos de integração.
  3. E substituímos o por

Mas de onde vêm essa regra de mudança para coordenadas polares?

Agora vou te explicar de onde vem as regras acima.

A primeira coisa que você tem que saber é que para mudar as coordenadas de uma integral dupla a gente só precisa substitui o e o pela nova coordenada, e multiplicar tudo pelo módulo do Jacobiano .

Vamos ver com calma o que isso significa na mudança para coordenadas polares.

Primeiro, vamos lembrar que em Coordenadas Polares nós representamos uma posição pelas variáveis , que é distância em linha reta até a origem, e o ângulo dessa distância.

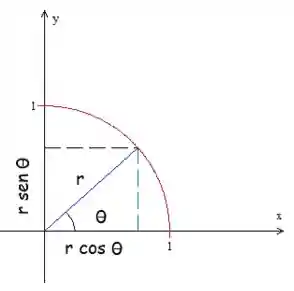
Coordenadas cartesianas
Coordenadas cartesianas

Agora, nota que legal. Se agente usar trigonometria, a gente pode relacionar a posição com a posição :

E é assim que a gente encontra a forma de substituir e por relações envolvendo e

Agora a gente precisa resolver a Matriz Jacobiana.

Aplicando os valores e dentro do jacobiano, e resolvendo as derivadas e o determinante vamos ter que:

E isso vale pra qualquer função que vamos converter em coordenada polar. Resultando em:

Quando usar mudança para coordenada polar?

Se um problema envolver uma circunferência ou curvas, então, usar coordenadas polares vai ser uma boa ideia.

Quando você ver integrais que envolvam é quase certo que usar coordenadas polares vai ajudar!

Exemplo

Calcule a integral onde

Passo 1: Aqui a gente tem a função então vamos aplicar a conversão e

Chegamos em:

Passo 2: Agora vamos cuidar dos limite de integração.

Observando a equação do circulo é um círculo centrado na origem e um raio 1.

Logo já sabemos que a variável estará contida no intervalo .

Além disso, esse é um círculo completo. E para darum giro completo do círculo é preciso ir de até . Então, sabemos que podemos conter no intervalo

Passo 3: Agora vamos aplicar o e os limites dos passos anteriores, e substituir por que vamos ter nossa integral em coordenada polar

Passo 4: Agora é só calcular a integral:

Integrando em :

Integrando em :

Que resulta em:

E é isso? Que tal ver um vídeo maneiro sobre o assunto?

Quer mais? Então, aqui em baixo tem uns exercícios pra você praticar 👇

Quando usar mudança para coordenada polar?

Exercícios Resolvidos

Exercício Resolvido #1

Diomara Pinto e Maria Cândida Ferreira Morgado, Cálculo Diferencial e Integral de Funções de Várias Variáveis, 3ª ed. Rio de Janeiro: UFRJ, 2009, pp. 181

Calcule ∬ D   l n ⁡ ( x 2 + y 2 )   d x d y , onde D é a região do primeiro quadrante situada entre as circunferências x 2 + y 2 = 1 e x 2 + y 2 = 4 .

Passo 1

Para resolver essa integral dupla, nós precisamos encontrar os limites de integração. Repara que o enunciado disse a região que estão integrando esta delimitada por no primeiro quadrante de duas circunferências. Sendo assim, é uma boa usar coordenadas polares para definirmos esses limites.

A mudança de coordenadas polares que faremos será:

x = r cos ⁡ θ

y = r sen ⁡ θ

Lembrando, que qualquer mudança de variável, implica em multiplicar a função da integral pelo Jacobiano. Nas coordenadas polares, o Jacobiano dessa transformação sempre será J = r .

Passo 2

Agora vamos analisar os intervalos de integração! O enunciado forneceu duas equações:

x 2 + y 2 = 1

x 2 + y 2 = 4

A primeira corresponde a uma circunferência de raio igual a 1 . Já a segunda, é uma circunferência de raio igual a 2 .

O problema também diz que a região está limitada no primeira quadrante. Então a região que estamos estudando será essa abaixo:

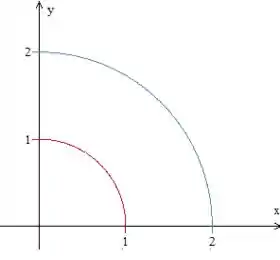
Repara que o raio r varia entre 1 e 2 e o ângulo θ entre 0 e π / 2 .

Passo 3

Agora que encontramos os limites de integração, vamos substituir na integral. Lembrando que a integral que estamos resolvendo tem essa cara:

∬ D   l n ⁡ ( x 2 + y 2 )   d x d y

Vamos, então, montar a integral, substituindo os valores que atribuímos a x e y :

∫ 1 2   ∫ 0 π 2 ln ⁡ r cos ⁡ θ 2 + r sen ⁡ θ 2 r d θ d r =

∫ 1 2   ∫ 0 π 2 r ln ⁡ r 2 ⁡ d θ d r

Não podemos esquecer o Jacobiano. Esse r que está multiplicando a função vem do Jacobiano!

Passo 4

Agora partiu resolver a integral!

∫ 1 2   ∫ 0 π 2 r ln ⁡ r 2 ⁡ d θ d r

Vamos começar integrando em relação a θ :

= ∫ 1 2   r ln ⁡ r 2 θ θ = 0 θ = π / 2 d r =

= π 2 ∫ 1 2 r ln ⁡ r 2   d r =

Mas ln ⁡ r 2 = 2 ln ⁡ r . Então, no fim, fica:

= π 2 ∫ 1 2 2 r ln ⁡ r   d r

= π ∫ 1 2 r ln ⁡ r   d r

Passo 5

Para integrar em relação a r , vamos fazer a integração por partes, com:

ln ⁡ r = u

r = v '

O que nos dá:

u ' = 1 r

v = r 2 2

Substituindo esses valores em ∫ u v ' = u v - ∫ u ' v

Temos:

∫ r ln ⁡ r d r = r 2 2 ln ⁡ r - ∫ 1 r × r 2 2 d r = r 2 2 ln ⁡ r - r 2 4

Então, o valor da nossa integral é:

π ∫ 1 2 r ln ⁡ r   d r = π r 2 2 ln ⁡ r - r 2 4 r = 1 r = 2 =

= π 4 2 ln ⁡ 2 - 4 4 - 1 2 ln ⁡ 1 - 1 4 =

= π 2 ln ⁡ 2 - 1 + 1 4 =

π 2 ln ⁡ 2 - 3 4

Resposta

π 2 ln ⁡ 2 - 3 4

Exercício Resolvido #2

CEFET - Cálculo 2 - P2 Roberto Sa 2012.1 – 1a

Calcule

∫ 0 1 ∫ 0 1 - y 2 cos ⁡ ( x 2 + y 2 ) d x d y

Passo 1

Antes de tudo, vamos analisar com calma aqui rapidinho. Repare que x varia desde x = 0 até x = 1 - y 2 e essa expressão nada mais é do que a parte com x positivo da circunferência x 2 + y 2 = 1 .

No termo que vamos integrar, temos x 2 e y 2 . Já entendeu onde queremos chegar? Isso tudo indica que a boa aqui é usar coordenadas polares. Vamos fazer isso então!

x = r   c o s   θ

y = r   s e n   θ

Como já vimos, o Jacobiano dessa transformação é J = r .

Passo 2

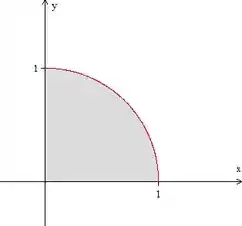
Para a gente não se confundir, vamos desenhar essa região de integração e descobrir os intervalos de r e θ , ok? Como já falamos, x varia desde 0 até um arco de circunferência. Olhando para a integral, vemos que y varia de 0 até 1 . Então temos:

É isso aqui o que temos então. Agora ficou mais fácil de ver que 0 ≤ r ≤ 1 e 0 ≤ θ ≤ π / 2 (o equivalente a 1 / 4 de volta do círculo).

Passo 3

Vamos, então, montar a integral, substituindo os valores que atribuímos a x e y :

∫ 0 1   ∫ 0 π 2 c o s r   c o s   θ 2 + r   s e n   θ 2 r d θ d r =

Esse r vem do Jacobiano!

= ∫ 0 1   ∫ 0 π 2 r   c o s ⁡ ( r 2 ) d θ d r =

Passo 4

Vamos começar integrando em relação a θ :

= ∫ 0 1   θ   r   c o s ⁡ ( r 2 ) 0 π / 2 d r =

= π 2 ∫ 0 1   r   c o s ⁡ ( r 2 ) d r =

Passo 5

Agora integramos em relação a r . Para isso, vamos fazer a substituição:

r 2 = u

2 r d r = d u

= π 2 ∫ 0 1   c o s ⁡ ( r 2 ) r   d r ⏟ d u / 2 =

= π 4 ∫ 0 1   c o s ⁡ ( u ) d u =

= π 4   s e n   u 0 1 =

= π 4   s e n   1

Resposta

π 4   s e n   1

Exercício Resolvido #3

UNICAMP - Cálculo 2 - P2 2013 Noite – 1

Calcule

∬ R   y d A

Onde R é a região no primeiro quadrante limitada pelo semi-círculo x 2 + y 2 = 2 x .

Passo 1

Bom, antes de tudo, vamos desenhar essa região R , para ter uma ideia melhor do que está acontecendo. Rearrumando a equação da circunferência:

x - 1 2 + y 2 = 1

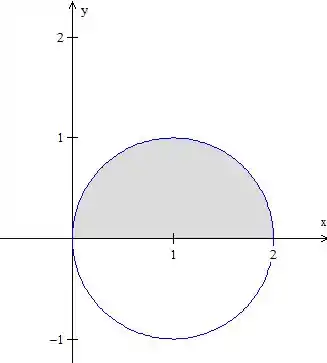
Portanto, é uma circunferência de raio 1 centrada em ( 1,0 ) . Temos isso aqui então:

A região R é essa em cinza.

Passo 2

Agora, vamos descrever essa região em coordenadas polares (já que se trata de um círculo):

x = r cos ⁡ θ

y = r   s e n   θ

J = r

Fazendo a mudança na equação da circunferência:

r cos ⁡ θ - 1 2 + r   s e n   θ 2 = 1

r 2 cos 2 ⁡ θ - 2 r cos ⁡ θ + 1 + r 2 s e n 2 θ = 1

r 2 = 2 r cos ⁡ θ

r = 2 cos ⁡ θ

Como o raio varia desde a origem até a equação da circunferência, temos:

0 ≤ r ≤ 2 cos ⁡ θ

Ainda olhando para o desenho, como a região está toda descrita no primeiro quadrante, temos que

0 ≤ θ ≤ π 2

Passo 3

Agora vamos montar a integral em coordenadas polares, fazendo a substituição:

x = r cos ⁡ θ

y = r   s e n   θ

J = r

∬ R   y d A = ∫ 0 π 2 ∫ 0 2 cos ⁡ θ r   s e n   θ r d r d θ

Temos, então:

= ∫ 0 π 2 ∫ 0 2 cos ⁡ θ r 2   s e n   θ d r d θ =

Passo 4

Agora é só resolver isso aí:

= ∫ 0 π 2 r 3 3 s e n   θ 0 2 cos ⁡ θ d θ =

= 1 3 ∫ 0 π 2 8 cos 3 ⁡ θ s e n   θ d θ =

= 8 3 ∫ 0 π 2 cos 3 ⁡ θ s e n   θ d θ =

Agora fazemos

cos ⁡ θ = u

- s e n   θ   d θ = d u

Mudando os limites de integração vai dar

θ = 0             →             u = 1

θ = π 2             →             u = 0

A nossa integral fica

= - 8 3 ∫ 1 0 u 3 d u =

= - 8 3 u 4 4 1 0 =

= - 8 3 0 - 1 4 =

= 8 12 =

= 2 3

Resposta

2 3

Exercício Resolvido #4

UNICAMP - Cálculo 2 - P2 2013 Tarde - 1

Utilize coordenadas polares para calcular

∬ R   x x 2 + y 2 d A

Onde

R = ( x , y ) ∈ R 2 | x 2 + y 2 ≤ 4   e   x ≥ 1

Passo 1

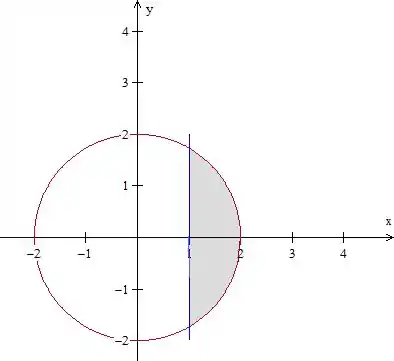
Bom, antes de tudo, vamos desenhar essa região R , para ter uma ideia melhor do que está acontecendo. Queremos a parte com x ≥ 1 do círculo de raio 2 :

Temos, então, essa região cinza.

Passo 2

Agora, vamos descrever essa região em coordenadas polares.

x = r cos ⁡ θ

y = r   s e n   θ

J = r

Como o raio vai desde a reta x = 1 até a circunferência de raio 2 , vamos fazer a mudança polar na reta:

x = 1 = r cos ⁡ θ

r = 1 cos ⁡ θ

Logo

1 cos ⁡ θ ≤ r ≤ 2

Agora, para achar o intervalo de θ , precisamos descobrir onde a reta corta a circunferência, ou seja, onde:

r = 1 cos ⁡ θ = 2

Isso ocorre se

cos ⁡ θ = 1 2

θ = π 3 - π 3

Logo, temos - π 3 ≤ θ ≤ π 3 .

Passo 3

Agora vamos montar a integral em coordenadas polares, fazendo a substituição:

x = r cos ⁡ θ

y = r   s e n   θ

J = r

∬ R   x x 2 + y 2 d A = ∫ - π 3 π 3 ∫ 1 cos ⁡ θ 2 r cos ⁡ θ r 2 r d r d θ

Temos, então:

= ∫ - π 3 π 3 ∫ 1 cos ⁡ θ 2 cos ⁡ θ d r d θ =

Passo 4

Agora é só resolver isso aí:

= ∫ - π 3 π 3 r cos ⁡ θ 1 cos ⁡ θ 2 d θ =

= ∫ - π 3 π 3 2 cos ⁡ θ - 1 d θ =

= 2   s e n   θ - θ - π 3 π 3 =

= 2 3 2 - π 3 - - 2 3 2 + π 3 =

= 2 3 - 2 π 3

Resposta

2 3 - 2 π 3

Exercício Resolvido #5

UFRJ - Cálculo 3 - P1 2011.1 - 1b

b) Calcule a integral

∫ 0 a cos ⁡ b   ∫ 0 x tg ⁡ b f ( x , y ) d y d x + ∫ a cos ⁡ b a   ∫ 0 a 2 - x 2 f ( x , y ) d y d x

Considerando f x , y = x 4 - y 4

Passo 1

Como temos termos quadráticos tanto no domínio como na função a ser integrada, vamos utilizar coordenadas polares. Faremos:

x = r cos ⁡ θ

y = r sen ⁡ θ

J = r

Passo 2

Primeiro vamos passar a nossa função f pra coordenadas polares

f = x 4 - y 4 = r cos ⁡ θ 4 - r sen ⁡ θ 4 = r 4 cos 4 ⁡ θ - sen 4 ⁡ θ

O que dá uma facilitada na nossa vida é fazer uma diferença de quadrados no termo entre parênteses

cos 4 ⁡ θ - sen 4 ⁡ θ = cos 2 ⁡ θ - sen 2 ⁡ θ cos 2 ⁡ θ + sen 2 ⁡ θ

Reconhece o segundo termo? É a identidade fundamental da trigonometria, ou seja, é igual a 1! Já o primeiro pode ser reescrito usando arco duplo pra cosseno

cos ⁡ 2 θ = cos 2 ⁡ θ - sen 2 ⁡ θ

Então

cos 4 ⁡ θ - sen 2 ⁡ θ = cos ⁡ 2 θ 1 = c o s ⁡ ( 2 θ )

Agora a nossa função f ficou com uma cara mais simpática :)

f = r 4 cos ⁡ 2 θ

Então finalmente podemos reescrever os que tá dentro dos nossos integrandos como

x 4 - y 4 d x d y = r 4 cos ⁡ 2 θ r d r d θ = r 5 cos ⁡ 2 θ d r d θ

Show!

Passo 3

Agora precisamos determinar os limites de integração!

Primeiro vamos olhar a primeira integral. Nela a variável y vai de 0 até x tan ⁡ b , então

0 < y < x tan ⁡ b

0 < r sen ⁡ θ < r cos ⁡ θ tan ⁡ b

0 < tan ⁡ θ < tan ⁡ b

Supondo que b > 0 , podemos dizer que

0 < θ < b

Uhul!

Já a coordenada x : essa coordenada vai de 0 até a cos ⁡ b , então

0 < x < a cos ⁡ b

0 < r cos ⁡ θ < a cos ⁡ b

0 < r < a cos ⁡ b cos ⁡ θ

Show! Como escrevemos os limites de r como uma função de θ então vamos primeiro integrar em r e depois em θ , beleza?

Passo 4

A primeira integral então fica

∫ 0 b ∫ 0 a cos ⁡ b / cos ⁡ θ r 5 cos ⁡ 2 θ d r   d θ

= ∫ 0 b cos ⁡ 2 θ r 6 6 0 a cos ⁡ b cos ⁡ θ d θ = 1 6 ∫ 0 b cos ⁡ 2 θ a 6 cos 6 ⁡ b cos 6 ⁡ θ d θ

= a 6 cos 6 ⁡ b 6 ∫ 0 b cos ⁡ 2 θ cos 6 ⁡ θ d θ

Agora temos que fazer essa integralzinha rsrsrsrs

Pra isso vamos reescrever

cos ⁡ 2 θ = cos 2 ⁡ θ - sen 2 ⁡ θ = 2 cos 2 ⁡ θ - 1

Então a integral fica

a 6 cos 6 ⁡ b 6 ∫ 0 b 2 cos 2 ⁡ θ - 1 cos 6 ⁡ θ d θ = a 6 cos 6 ⁡ b 6 ∫ 0 b ( 2 sec 4 ⁡ θ - sec 6 ⁡ θ )   d θ

Essa integral é beeemm chatinha. O resultado dela é

= a 6 cos 6 ⁡ b 6 1 10 6 cos ⁡ 2 θ + cos ⁡ 4 θ + 3 tan ⁡ θ sec 4 ⁡ θ 0 b

Lembrando que tan ⁡ 0 = 0

= a 6 cos 6 ⁡ b 6 1 10 6 cos ⁡ 2 b + cos ⁡ 4 b + 3 tan ⁡ b sec 4 ⁡ b

= a 6 cos ⁡ b sen ⁡ b 60 6 cos ⁡ 2 b + cos ⁡ 4 b + 3

Show!

Passo 5

Agora vamos pra segunda integral!

A coordenada y é limitada por

0 < y < a 2 - x 2 → 0 < r sen ⁡ θ < a 2 - r 2 cos 2 ⁡ θ

E a coordenada x é limitada por

a cos ⁡ b < x < a

a < r cos ⁡ θ < a cos ⁡ b

Meio complicado, né? O engraçado é que nessa integral é mais fácil usar as coordenadas cartesianas mesmo ¯¯\_(ヅ)_/¯

∫ a cos ⁡ b a   ∫ 0 a 2 - x 2 x 4 - y 4 d y d x = ∫ a cos ⁡ b a x 4 y - y 5 5 0 a 2 - x 2   d x

= ∫ acos ⁡ b a x 4 a 2 - x 2 - a 2 - x 2 5 d x

∫ acos ⁡ b a a 2 - x 2 x 4 - a 2 - x 2 4 d x

O que tá dentro dos colchetes fica

x 4 - a 2 - x 2 4 = x 4 - a 2 - x 2 2 = x 4 - a 4 - 2 a 2 x 2 + x 4 = 2 a 2 x 2 - a 4

Assim

∫ acos ⁡ b a a 2 - x 2 2 a 2 x 2 - a 4 d x = 2 a 2 ∫ acos ⁡ b a a 2 - x 2 x 2 d x - a 4 ∫ acos ⁡ b a a 2 - x 2 d x

De novo, uma integrais chatinhas haha

= 2 a 2 8 x a 2 - x 2 2 x 2 - a 2 + a 4 arctan ⁡ x a 2 - x 2 - a 4 2 x a 2 - x 2 + a 2 arctan ⁡ x a 2 - x 2 a a cos ⁡ b

= a 2 4 a cos ⁡ b a 2 - a 2 cos 2 ⁡ b 2 a 2 cos 2 ⁡ b - a 2 + a 4 arctan ⁡ acos ⁡ b a 2 - a 2 cos 2 ⁡ b - a 4 2 a cos ⁡ b a 2 - a 2 cos 2 ⁡ b - a 6 2 arctan ⁡ acos ⁡ b a 2 - a 2 cos 2 ⁡ b

Vamos reescrever as raízes como

a 2 - a 2 c o s 2 b = a 1 - cos 2 ⁡ b = a sen 2 ⁡ b = a sen ⁡ b

E esses arcos tangentes

arctan ⁡ acos ⁡ b a 2 - a 2 cos 2 ⁡ b = arctan ⁡ a cos ⁡ b a sen ⁡ b = arctan ⁡ c o t a n   b

Então finalmente

= a 6 4 cos ⁡ b sen ⁡ b 2 cos 2 ⁡ b - 1 + a 6 4 arctan ⁡ c o t a n   b - a 6 2 cos ⁡ b sen ⁡ b - a 6 2 arctan ⁡ c o t a n   b

= a 6 4 cos ⁡ b sen ⁡ b 2 cos 2 ⁡ b - 3 - arctan ⁡ c o t a n   b

Ufa hahaha!

Passo 6

Agora é só juntar tudo depois de toda essa sofrência hahaha

a 6 cos ⁡ b sen ⁡ b 60 6 cos ⁡ 2 b + cos ⁡ 4 b + 3 + a 6 4 cos ⁡ b sen ⁡ b 2 cos 2 ⁡ b - 3 - arctan ⁡ c o t a n   b

Feshow? :D

Resposta

a 6 cos ⁡ b sen ⁡ b 60 6 cos ⁡ 2 b + cos ⁡ 4 b + 3 + a 6 4 cos ⁡ b sen ⁡ b 2 cos 2 ⁡ b - 3 - arctan ⁡ c o t a n   b

Exercício Resolvido #6

UERJ - Cálculo 2 - Lista do Hamilton - Integral Dupla - 4b

Calcular a área da região abaixo usando integral dupla

x , y ∈ R 2 x 2 + y 2 + 8 y ≤ 0   e   x 2 + y 2 ≥ 16

Passo 1

Bom, antes de tudo vamos fazer um esboço dessa região para entender melhor o que está acontecendo e depois partimos para integral.

Começando pela inequação:

x 2 + y 2 ≥ 16

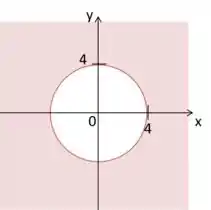
Essa é uma circunferência de raio r = 4 centrada na origem e, como vemos pela inequação (o sinal ≥ ), a região que queremos está fora dela (indicado em vermelho no gráfico abaixo).

Passo 2

Temos também a seguinte inequação:

x 2 + y 2 + 8 y ≤ 0

Que curva é essa? Se não fosse pelo termo 8 y , você pensaria direto em uma circunferência, não é? E realmente é um circunferência, esse termo 8 y apenas nos diz que ela não está centrada na origem.

Sempre que você vir uma equação desse tipo, com um termo quadrático e um simples da mesma variável ( y 2 e 8 y ) é uma boa tentar juntar esses termos, completando o quadrado que eles formam. Como assim?

Queremos escrever o termo y 2 + 8 y na forma y + a 2 , completando o que for necessário. Desenvolvendo esse quadrado, temos:

y + a 2 = y 2 + 2 a y + a 2

Se nós fizermos a = 4 , temos:

y + 4 2 = y 2 + 8 y ⏟ + 16

Esses dois primeiros termos estão presentes na nossa inequação, o último não, mas beleza. Vamos substituir y 2 + 8 y por y + 4 2 , mas como sinifica adicionar um termo " + 16 " que não estava lá antes, vamos retirar esse termo, ok? Olha só:

x 2 + y + 4 2 ⏟ y 2 + 8 y + 16 - 16 ≤ 0

Assim não alteramos a inequação, certo? Beleza, então temos:

x 2 + y + 4 2 ≤ 16

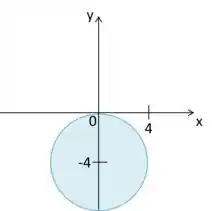
Isso é uma circunferência de raio r = 4 , como previmos, não centrada na origem (ela está centrada em ( 0 , - 4 ) ). Como vemos pela inequação (o sinal ≤ ) a região que queremos está dentro dela.

Portanto, juntando os dois gráficos temos isso aqui:

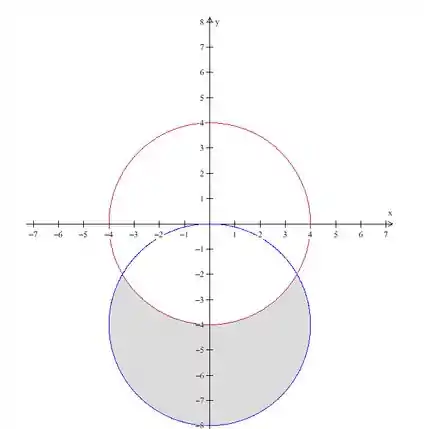
Passo 3

Como nós queremos a área da região, precisamos resolver a seguinte integral:

área D = ∬ D   d x d y

Onde D é a região marcada em cinza na figura.

Como a região é limitada por círculos, vamos usar coordenadas polares aqui:

x = r cos ⁡ θ

y = r sen ⁡ θ

Sempre que mudamos de coordenadas nas integrais duplas, precisamos calcular o Jacobiano dessa transformação, neste caso temos

J = ∂ ( x , y ) ∂ ( r , θ ) = ∂ x ∂ r ∂ x ∂ θ ∂ y ∂ r ∂ y ∂ θ

J = cos ⁡ θ - r   s e n θ s e n   θ r   c o s   θ = r   c o s 2 θ + r   s e n 2 θ = r [ c o s 2 θ + s e n 2 θ ]

J = r

A equação da circunferência vermelha x 2 + y 2 = 16 se transforma então em r = 4 . Veja,

r cos ⁡ θ 2 + r   sen ⁡ θ 2 = 16

r 2 ( s e n 2 θ + c o s 2 θ ) = 16

r 2 = 16

r = 4

Agora vamos fazer essa substituição na outra circunferência x 2 + y + 4 2 = 16 :

r cos ⁡ θ 2 + r   sen ⁡ θ + 4 2 = 16

r 2 cos 2 ⁡ θ + r 2 sen 2 ⁡ θ + 8 r sen ⁡ θ + 16 = 16

r 2 ( s e n 2 θ + c o s 2 θ ) + 8 r sen ⁡ θ + 16 = 16

r 2 + 8 r sen ⁡ θ = 0

r = - 8 sen ⁡ θ

Passo 4

Beleza, agora vamos olhar um pouco para a figura. Repare que, dentro da nossa região D , temos o raio variando desde a circunferência vermelha até a azul, portanto:

4 ≤ r ≤ - 8 sen ⁡ θ

Não está errado esse sinal " - " não? Não, porque abaixo do eixo y ,   sen ⁡ θ tem valores negativos, portanto, - sen ⁡ θ é um número positivo.

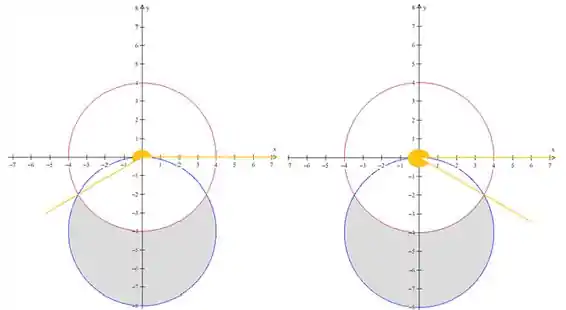
Beleza, agora vamos analisar o intervalo de θ . Antes de sair chutando, dá uma olhada de novo a figura da nossa região D . Lembra que θ é marcado em relação à parte positiva do eixo x ? Queremos então esses ângulos aqui em amarelo:

Mas como vamos descobrir esses ângulos? Bom, esses ângulos batem exatamente na interseção das duas curvas né? Então que tal acharmos essa interseção! Vamos começar substituindo logo x = r cos ⁡ θ e y = r sen ⁡ θ nas funções:

x 2 + y 2 + 8 y = 0 ⇒ r 2 + 8 r sin ⁡ θ = 0

x 2 + y 2 = 16 ⇒ r 2 = 16 ⇒ r = 4

Substituindo r = 4 na primeira equação:

16 + 32 sen ⁡ θ = 0

sin ⁡ θ = - 0 , 5

E qual ângulo têm o seno igual a - 0 , 5 ? 30 ° . Mas aqui estamos abaixo do eixo x .

Então primeiro temos,

180 ° + 30 ° = π + π 6 = 7 π 6

Mas também vamos ter,

360 ° - 30 ° = 2 π - π 6 = 11 π 6

Logo, chegamos à conclusão de que

7 π 6 ≤ θ ≤ 11 π 6

Passo 5

Nós descobrimos então que, em coordenadas polares, podemos escrever essa região como:

{ r , θ   ϵ   R 2 | 210 ° ≤ θ ≤ 330 ° ; 4 ≤ r ≤ - 8 sen ⁡ θ }

Vamos então fazer finalmente essa substituição polar na integral (não se esqueça do Jacobiano):

área D = ∬ D   d x d y = ∫ 7 π 6 11 π 6 ∫ 4 - 8 sen ⁡ θ r   d r d θ

Passo 6

Agora vamos integrar isso aí em relação a r :

∫ 7 π 6 11 π 6 ∫ 4 - 8 sen ⁡ θ r   d r d θ = ∫ 7 π 6 11 π 6   r 2 2 4 - 8 sen ⁡ θ d θ =

= 1 2 ∫ 7 π 6 11 π 6 64 sen 2 ⁡ θ - 16   d θ =

= ∫ 7 π 6 11 π 6 32 sen 2 ⁡ θ - 8   d θ =

Passo 7

Agora integramos em relação a θ , mas antes disso, precisamos nos lembrar da seguinte relação:

sen 2 ⁡ θ = 1 - cos ⁡ 2 θ 2

Isso nos dá

= ∫ 7 π 6 11 π 6 16   1 - cos ⁡ 2 θ - 8   d θ =

= ∫ 7 π 6 11 π 6 - 16   cos ⁡ 2 θ + 8   d θ =

= - 8 sen ⁡ 2 θ + 8 θ 7 π 6 11 π 6 =

= 8 - sen ⁡ 11 π 3 + 11 π 6 - - sen ⁡ 7 π 3 + 7 π 6   =

= 8 - sen ⁡ 6 π 3 + 5 π 3 + 2 π 3 + sen ⁡ 6 π 3 + π 3   =

= 8 - sen ⁡ 2 π + 5 π 3 + 2 π 3 + sen ⁡ 2 π + π 3   =

= 8 - sen ⁡ 5 π 3 + 2 π 3 + sen ⁡ π 3   =

Agora vamos lá:

π 3 = 60 °         →         sen ⁡ π 3 = sen ⁡ 60 ° = 3 2

5 π 3 = 300 °         →       sen ⁡ 5 π 3 = sen ⁡ 300 ° = - sen ⁡ 60 ° = - 3 2

Substituindo:

= 8 3 2 + 2 π 3 + 3 2   =

= 16 π 3 + 8 3

Resposta

16 π 3 + 8 3

Exercícios de Livros Relacionados

Determine todos os valores de p para os quais I p , a tem um limite finito quando a tende para + ∞ .
Se a0 , seja I (a) = int_(- a)^a e^(- u^2) d u .Mostre queI^2 (a) = int int_D e^(- (x^2 + y^2)) d x d y Onde:D = [- a , a] xx [- a , a]
Se a0 , seja I a = ∫ - a a e - u 2 d u .Se B 1 e B 2 são bolas inscrita e circunscrita a D , respectivamente mostre que ∫ ∫ B 1 e - x 2 + y 2 d x d y ≤ I 2 a ≤ ∫ ∫ B 2 e - x 2 + y 2 d x d y
Determine o volume dos sólidos W abaixo. W é limitado pelas superfícies z = x 2 + y 2 , x 2 + y 2 = 4 , x 2 + y 2 = 9 e o plano z = 10 .
Calcule int int_D (e^(((x + y)/(x - y))))/((x - y)^2) d x d y , ondeD = {(x , y) in R^2,1 = (x - y)^2 = 4 , y = 0 e x + y = 0}