Use uma ferramenta gráfica para fazer o gráfico de .
Começando com o gráfico da parte , esboce um gráfico da primitiva que satisfaça .
Use as regras dessa seção para achar uma expressão para .
Faça o gráfico de usando a expressão da parte . Compare com seu esboço da parte .
Passo 1
Fala aí, pessoal.
Bom, essa questão quer que estudemos o comportamento de uma função através de suas informações gráficas. Pra isso precisaremos responder quatro diferentes itens. Vejamos:
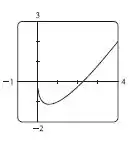
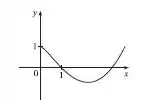
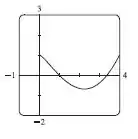
No item a) precisaremos usar uma ferramenta gráfica para fazer o gráfico da função:
Depois disso, seguiremos para o item b). Onde, usando o gráfico do item a), vamos esboçar um novo gráfico da primitiva que satisfaça .
Aqui temos que lembrar que a primitiva de uma determinada função, nada mais é que uma função que, ao ser derivada, tem como resultado a função dada.
Então, sabendo que
Podemos analisar seus sinais, e descobrir algumas informações importantes sobre a função , já que:

No item c), precisaremos usar as regras da sessão para achar uma expressão para . E as regras ao qual o enunciado se refere são as regras para encontrar a primitiva de uma função de acordo com suas características. E temos a seguinte tabelinha para nos ajudar:

E no item d), faremos o gráfico de usando a expressão da parte c). Depois vamos comparar nosso resultado com seu esboço da parte b).
Agora que já sabemos o que fazer, vamos ver como fica isso no passo a passo.
Vem comigo.
Passo 2
Item a). Vamos começar esboçando graficamente a função
E teremos o seguinte gráfico:
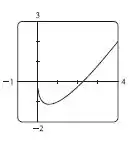
Passo 3
Agora, no item b) podemos esboçar um novo gráfico da primitiva que satisfaça , usando o gráfico anterior para tirarmos algumas conclusões.
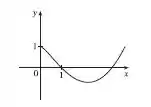
Como , começamos o gráfico em .
Como

No ponto onde nossa função possui um mínimo local temos um ponto onde a derivada é nula.
Dessa forma, esse ponto é um ponto de inflexão da nossa primitiva.
Nos intervalos onde nossa função é negativa, deveremos ter um decrescimento da primitiva e nos intervalos onde a função é positiva deveremos ter um crescimento da primitiva.
Podemos assim esboçar o seguinte gráfico
Passo 4
Agora, no item c) iremos encontrar a equação da primitiva com base em .
Olhando a tabela de primitivas, vemos que:
![]()
É a regra mais indicada, então vamos reescrever nossa função colocando a raiz de como uma potência de expoente fracionário. Assim:
E sua primitiva será:
Ou melhor:
Perceba que derivando temos
Dessa forma, como , então é a primitiva de . Podemos encontrar o valor da constante aplicando a seguinte condição
Dessa forma, temos
Passo 5
Agora, no item d) esboçando o gráfico de , temos
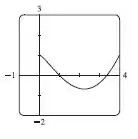
Que condiz com o esboço do item .
E prontinho.
Resposta