37-a) Use um recurso gráfico computacional para gerar o gráfico da função e, então use o gráfico para fazer uma conjectura sobre o número e a localização de todas as descontinuidades.

b)Verifique sua conjectura fatorando o denominador.

a)Galera, nós temos o seguinte gráfico:

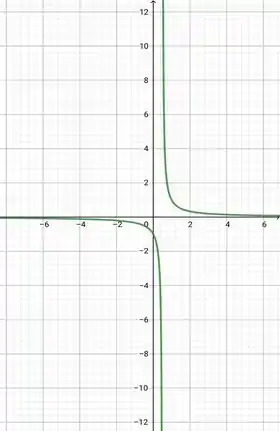
Nós descontinuidades em e . Onde nós temos em uma descontinuidade removível e em não removível.

Olha só, se nós calculássemos o limite da função quando x tende a -3, teríamos:

Dessa forma, poderíamos definir uma função g(x), contínua em , e que coincide com para todo , o que torna o -3 uma descontinuidade removível.

No caso do , não existe . Portanto, mesmo que a gente defina uma função definida em , com algum valor de , nunca teremos . Dessa forma, para temos uma descontinuidade removível.