Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 2.5 - Ex. 41
Encontre os pontos nos quais é descontínua. Em quais desses pontos é contínua à direita, à esquerda ou nenhum deles? Esboce o gráfico de .
Passo 1
Olá, meu amigo. Yuri aqui e estarei te ajudando a resolver essa querida atividade.
O enunciado pede para identificar os pontos de descontinuidade e em seguida classifica-los quanto a continuidade lateral. Antes de mais nada, devemos observar que é definida por partes e que suas partes são funções contínuas. Assim, os possíveis pontos de descontinuidade são os pontos de “colagem”. Pontos em que temos as transições entre as funções que compõem nossa função.
Vale lembrar também que uma função é contínua lateralmente em um ponto se o limite lateral coincidir com o valor da função no ponto em questão.
Passo 2
Os pontos de “colagem” são e . Primeiramente vamos analisar o que acontece em .
À esquerda desse ponto (), , assim o limite lateral à esquerda é
À direita (), , de modo que:
Como os limites laterais são diferentes, não existe e é descontínua nesse ponto. Por outro lado, como , é contínua à esquerda nesse ponto.
Passo 3
Analisemos agora o que acontece em . O limite à esquerda será
O limite à direita será:
Como os limites laterais são iguais, o limite existe e vale 0:
Além disso, como , é contínua nesse ponto.
Passo 4
Para o esboço do gráfico de vamos pegar os pontos onde até . Vamos utilizar o nosso amigo GeoGebra para nos ajudar com isso:
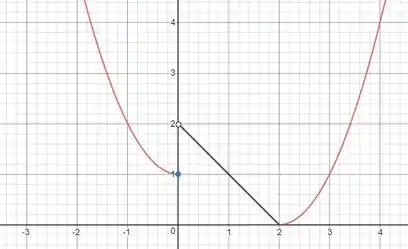
Resposta
R: O único ponto de descontinuidade de é . Neste ponto, é contínua à esquerda.