Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.5 - Ex. 10
9-10. Encontre uma equação da parábola. A seguir, ache o foco e a diretriz.
Passo 1
De acordo com a seção 10.5 do Stewart, a equação que define o comportamento de uma parábola é a seguinte:
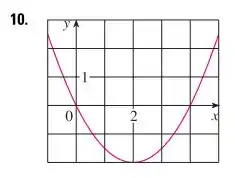
No entanto, essa equação SÓ é válida para parábolas com vértice na origem, ou seja, em ! Se observarmos o gráfico que nos foi dado notaremos que o vértice da parábola não está na origem, ele está deslocado verticalmente e horizontalmente por algumas casas. Para esse tipo de caso, temos a seguinte equação:
No qual e se referem ao ponto no qual o vértice se encontra. Ademais, se observarmos o gráfico que nos foi dado com cuidado, podemos perceber que o vértice está no ponto , ou seja, duas casas para a direita e duas casas para baixo. Em outras palavras:
Substituindo na equação da parábola que escrevemos:
Passo 2
Tudo bem, agora encontramos uma expressão parcial dessa parábola, pois falta descobrirmos quanto vale , certo? Aqui vamos utilizar uma análise um pouco mais profunda do gráfico, mas nada tão difícil assim, beleza? Como não temos a expressão da parábola (é o que queremos descobrir), então temos que ver se o gráfico dado nos cede algum ponto, qualquer um! Podemos notar que a curva passa pela origem, ou seja, em , não é mesmo? Se substituirmos esse ponto na equação “parcial” da parábola que encontramos, teremos:
Opa, agora sim! Substituindo , teremos:
Sendo assim, está aí a equação da nossa parábola de forma completa!
Passo 3
Por fim, para determinarmos o foco e a diretriz temos que utilizar as seguintes relações:
Aqui vale ressaltar que essas relações só estão sendo utilizadas porque a parábola está deslocada, tudo bem? Se a parábola tivesse seu vértice na origem, e , então se resumiria a:
Mas isso é só um conceito a mais para ficar aí pra vocês, belezura? Substituindo os valores que temos para descobrirmos o foco e a diretriz, teremos: