Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.4 - Ex. 27
Encontre a área da região que está dentro da primeira curva e fora da segunda curva.
27. ,
Passo 1
Olá, meu amigo. Vamos resolver essa atividade juntinhos hoje!!!!
Aqui a gente tem duas curvas em coordenadas polares:
E queremos calcular a área da região que está dentro da primeira curva e fora da segunda curva.
A segunda curva é a curva:
E a primeira curva é a:
Podemos ver pelo gráfico da imagem:
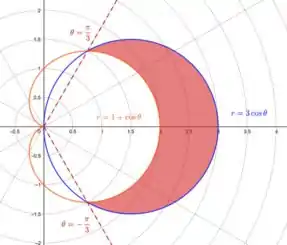
Queremos então calcular a área da região vermelha do nosso gráfico. Veja que para isso vamos ter que determinar quais os limites de integração.
Precisamos determinar o intervalo de em que esta região está contida, para isso, vamos igualar as duas equações, já que esse intervalo pode ser determinado pelos pontos de interseção das duas curvas.
Como a região é simétrica em relação ao eixo , podemos integrar no intervalo e multiplicar a integral da área por , que será equivalente ao que encontramos para o ângulo.
Veja também que o que temos ali é o cálculo da área de menos a área da região de
A integral da área pode ser escrita então como:
Passo 2
Primeiro iremos igualar as equações para encontrarmos os limites de integração:
Então nosso cálculo de área se torna:
Onde e
Passo 3
Vamos primeiro resolver a integral indefinida, e depois aplicamos os limites de integração:
Abrindo os polinômios:
Utilizando a seguinte propriedade trigonométrica:
Ficamos com:
Somando os termos:
Integrando:
Passo 4
Aplicando os limites, teremos: