Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 7.3 - Ex. 15

Avalie a integral.

int (x^2)/((a^2 - x^2)^((3)/(2))) d x

Passo 1

Para a resolução de uma integral pela substituição trigonométrica, precisamos fazer a escolha da substituição. Sendo x = a sin theta , onde - (pi)/(2) <= theta <= (pi)/(2) . Logo, derivando temos d x = a cos theta d theta . Assim podemos substituir!!

int (( a sin theta )^2 a cos theta d theta)/((a^2 - ( a sin theta )^2)^((3)/(2))) = int (( a sin theta )^2 a cos theta d theta)/(a^3 cos^3 theta)

Simplificamos a integral e teremos:

int (( a sin theta )^2 a cos theta d theta)/(a^3 cos^3 theta) = int (sin^2 theta)/(cos^2 theta) d theta

Isso nos mostra que a integral é:

int tan^2 theta d theta

Assim podemos usar a formula trigonométrica de tan^2 x = sec^2 x - 1

int ( sec^2 theta - 1 ) d theta

Essa integral tem como resultado:

int ( sec^2 theta - 1 ) d theta = tan theta - theta + C

Passo 2

Esboçando o triangulo retângulo associado, temos:

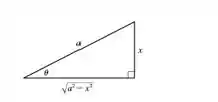
Então,

int (x^2)/((a^2 - x^2)^((3)/(2))) d x = (x)/(sqrt(a^2 - x^2)) - arcsin (x)/(a) + C

Prontinho!!

Resposta

int (x^2)/((a^2 - x^2)^((3)/(2))) d x = (x)/(sqrt(a^2 - x^2)) - arcsin (x)/(a) + C

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

a) int cos (x) root(3)(s e n (x)) d x
2. Seja f x uma função contínua. a) Mostre que a mudança de variável u = s e n ( x ) transforma a integral ∫ f s e n x ⋅ cos ⁡ x d x em ∫ f u d u
e) int (cos^3 ( x ))/(s e n^7 ( x )) d x
c) int (s e n (x))/(c o s^5 (x)) d x
d) int (s e n^3 (x))/(cos (x)) d x