Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.3 - Ex. 28
(a) Uma broca cilíndrica de raio é usada para fazer um furo que passa pelo centro de uma esfera de raio . Determine o volume do sólido em formato de anel resultante.
(b) Expresse o volume da parte (a) em termos da altura do anel. Observe que o volume depende somente de e não de ou .
Passo 1
Fala, galera! Tudo na paz?
A questão pede pra gente responder encontrar o volume do sólido do anel formado pela esfera que recebeu um furo. Como estamos lidando com regiões circulares, fica mais fácil trabalharmos com coordenadas polares.
O Volume do sólido é dado por:
Mas aqui no nosso caso, como temos coordenadas polares, vamos achar nossa equação e nossos limites de integração em relação a e a . Então aqui teremos:
Então para a parte a) vamos ter que achar a equação que descrever a forma de anel e seus limites de integração, assim a gente calcula a integral e obtém o volume da forma.
Aqui como um anel são dois círculos de mesmo centro, com um raio interno e um externo , podemos escrever nossa equação como:
Para a parte nós vamos reescrever a função o volume que achamos na parte a) em termos da altura do anel.
Vamo lá!
Passo 2
- Pessoal, pra calcular o volume desse sólido, temos que escrever uma integral dupla que o represente. Quando temos dois círculos concêntricos, a região em forma de anel é dada por:
ou seja
Como estamos falando de um círculo completo, a variação de é:
Aqui, vamos considerar só a parte positiva do sólido (acima do eixo ), por isso temos que multiplicar nosso volume por 2, pois assim vamos considerar o sólido todo e não só metade.
Para achar nosso integrando vamos ter nossa equação do anel:
Como a equação da esfera é:
Vamos isolar o :
Vamos substituir pela equação do círculo, pois no plano o sólido é uma circunferência:
Então o integrando será:
e, portanto, a integral será:
Podemos separar a integral no produto de duas integrais simples:
Resolvendo cada:
Aplicando os limites de integração:
Então:
Passo 3
(b) Show! Agora que já descobrimos a expressão do volume em termos de e , dê uma olhada na figura seguinte pra relacionarmos isso com a altura do anel, que representa a seção transversal do sólido:
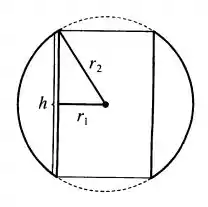
Vemos que forma um triângulo entre , e metade da altura . Então, usando Pitágoras, podemos escrever:
Logo, podemos reescrever o volume assim:
Realmente, o volume só depende de , não de ou !
Resposta
(a)
(b)