Enunciado
Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 1.1 - Ex. 13
Em cada um dos problemas de 11 a 14, desenhe um campo de direções para a equação diferencial dada.Baseado no campo de direções, determine o comportamento de y quando . Se esse comportamento depender do valor incial de , descreva essa dependência. Note que, nesses problemas, as equações não são da forma e o comportamento é um pouco mais complicado do que o das soluções das equações no texto
Passo 1
Campos de direções são ferramentas valiosas no estudo de soluções de equações diferenciais da forma
Em que é uma função dada de duas variáveis, , algumas vezes chamada de função taxa. Um campo de direções pode ser constuido calculando em cada ponto de uma malha retangular. Em cada ponto da malha desenha-se um pequeno segmento de reta cujo coeficiente angular é o valor da função naquele ponto.
Um campo de direções fornece uma boa ideia do comportamento global das soluções de uma equação diferencial.
Para construir campos de direções não precisamos resolver nossa EDO, basta calcular a função dada muitas vezes.
Passo 2
Nesse caso a nossa função de duas variáveis tem raíz dupla 0 . O coeficiente angular que representa os segmentos no campo de direções e vai obedecer o sinal de que é uma parábola com concavidade para cima, ou seja, como , então o coeficiente angular será sempre positivo idependente do valor inicial, de modo que o gráfico do campo de direções é o seguinte:
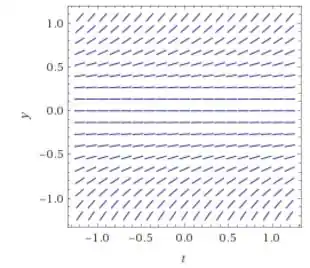
Passo 3
Portanto, se y for maior que 0 o coeficiente é positivo, logo estaria se afastando de 0. E para valores de y negativos,o campo de direções nos mostra que há uma convergência para zero, logo converge para zero.
Resposta
para valores iniciais negativos
para valores iniciais positivos