Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diva Flemming - Cálculo B - Ed: 2º - Capítulo 8.7 - Ex. 1

Calcular ∭ T ( x 2 + y 2 ) d V , onde T é a região interior ao cilindro x 2 + y 2 = 1 e à esfera x 2 + y 2 + z 2 = 4 .

Passo 1

Bora começar?!

Então galera, a primeira coisa a fazer aqui é tentar desenhar:

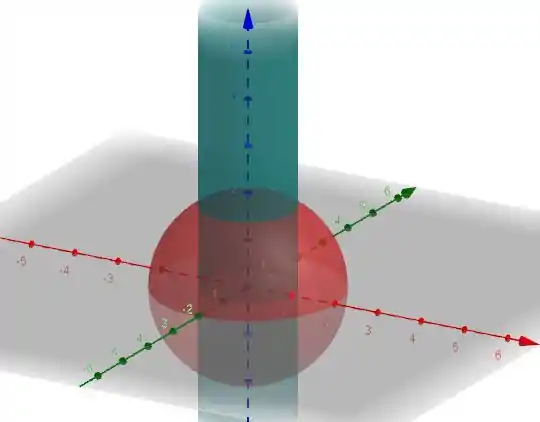
Sendo assim, z é limitada superiormente e inferiormente pela esfera x 2 + y 2 + z 2 = 4 .

Então nós vamos isolar z para achar os intervalos de integração:

z 2 = 4 - ( x 2 + y 2 )

z = ± 4 - ( x 2 + y 2 )

Sabendo que :

x 2 + y 2 = r 2

Então:

z = ± 4 - r 2

Passo 2

Agora que já sabemos os intervalos de integração, podemos usar a definição (4) para mudar as variáveis de integração:

∭ T ( x 2 + y 2 ) d V = ∬ R ∫ - 4 - r 2 4 - r 2 r 2 d z r d r d θ

Resolvendo:

∫ - 4 - r 2 4 - r 2 r 2 d z = r 2 z = r 2 4 - r 2 - ( - 4 - r 2 )

= 2 r 2 4 - r 2

Sendo assim:

= ∬ R 2 r ( 4 - r 2 ) 1 2 r d r d θ

= 2 ∬ R r 3 ( 4 - r 2 ) 1 2 d r d θ

Pelo cilindro nós sabemos que:

R : { 0 ≤ r ≤ 1 0 ≤ θ ≤ 2 π  

Aplicando na integral:

= 2 ∫ 0 2 π [ ∫ 0 1 r 3 4 - r 2 d r ] d θ  

Resolvendo a integral:

∫ 0 1 r 3 4 - r 2 d r

Para resolver vamos usar a substituição:

u = 4 - r 2 → r 2 = 4 - u 2

d u = 1 2 4 - r 2 - 1 2 . - 2 r d r →   d u = - r d r 4 - r 2 1 2 → d u = - r d r u 2 1 2 = - r d r u

- u . d u = r . d r

Substituindo:

∫ 0 1 r 3 4 - r 2 d r = ∫ 0 1 r 2 4 - r 2 r d r = ∫ 0 1 4 - u 2 . u . ( - u . d u )

= - ∫ 0 1 4 - u 2 . u 2 . d u = ∫ 0 1 u 4 . d u - ∫ 0 1 4 u 2 . d u

= u 5 5 - 4 u 3 3

Substituindo o u:

= ( 4 - r 2 ) 5 2 5 - 4 ( 4 - r 2 ) 3 2 3

Aplicando o intervalo:

= 4 - 1 5 2 5 - 4 - 0 5 2 5 - 4 4 - 1 3 2 3 - 4 4 - 0 3 2 3

= 9 3 5 - 32 5 - 4 3 3 3 - 8 3

= 9 3 5 - 32 5 - 4 3 - 8 3

Reorganizando:

= 9 3 - 32 5 - 4 3 3 - 8 3

= 9 3 - 32 5 + 4 8 - 3 3 3

= 9 3 - 32 5 + 32 - 12 3 3

Tirando o MMC:

= 27 3 - 96 + 160 - 60 3 1 5 = 64 - 33 3 15

Passo 3

= 2 ∫ 0 2 π 64 - 33 3 15 d θ  

= 2 . 64 - 33 3 15 ∫ 0 2 π d θ

= 2 . 64 - 33 3 15 θ

Aplicando o intervalo:

= 4 π 64 - 33 3 15

= π 256 15 - 44 3 5

O que acharam desta?

Resposta

π 256 15 - 44 3 5

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

∫ 0 2 π ∫ 0 θ 2 π ∫ 0 3 + 24 r 2 d zrd rd θ
∫ - 1 1 ∫ 0 2 π ∫ 0 1 + cos ⁡ θ 4 rd rd θd z
∫ 0 2 π ∫ 0 1 ∫ r 1 2 - r 2 3d zrd rd θ
∫ 0 π ∫ 0 θ π ∫ - 4 - r 2 3 4 - r 2zd zrd rd θ
∫ 0 1 ∫ 0 z ∫ 0 2 π ( r 2 cos 2 ⁡ θ + z 2 )rd θd rd z