Calculeint sqrt(9 - (x - 1)^2) d x

int sqrt(9 - (x - 1)^2) d x = (9)/(2) arcsin ((x - 1))/(3) + (x - 1) (sqrt(9 - (x - 1)^2))/(2) + k

Enunciado

Primeiro precisamos substituir:

A função dentro da integral é:

Não parece muito familiar?

Na verdade a resolução pra esse tipo de função é chamada substituição trigonométrica e funciona assim:

A gente pega um triângulo retângulo com ângulo como esse:

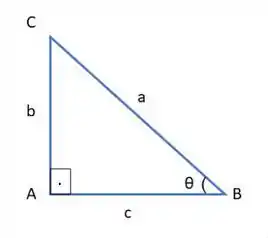
Agora imagine que um dos catetos vale 3, e o outro cateto vale , concorda comigo que a hipotenusa vai valer ?

Então que substituição poderíamos fazer?

Bem, se dissermos que então

Assim podemos substituir a integral dessa forma:

Ótimo! Agora podemos calcular essa integral de maneira mais fácil

Vamos agora lembrar que:

Vamos ficar com:

Vamos fazer uma substituição tal que:

Voltando pra variável :

Agora precisamos voltar pra variável , lembrando:

E que:

Assim:

E por fim voltar pra variável :