Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 7.3 - Ex. 13

Calcule a integral

int (sqrt(x^2 - 9))/(x^3) d x

Passo 1

Yuri aqui meu nobre e estarei te ajudando nessa caminhada.

Aqui temos uma integral para resolver.

Estas integrais são trabalhosas e você sempre vai precisar pensar, mas com MUITA prática você consegue e vai ver que vai conseguir pensar nas substituições só de bater o olho na integral.

Sugiro aqui utilizarmos então uma substituição trigonométrica. Pois nessas situações, como até a tabela abaixo nos mostra, é a nossa melhor opção.

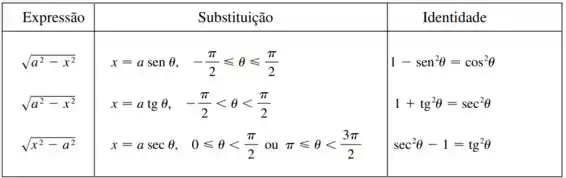
Sugiro o seguinte, vamos dizer que

x = 3 sec (theta)

Diferenciando, temos que

d x = 3 sec (theta) tan (theta) d theta

Tudo beleza?! Vamos substituir isso na nossa integral

Passo 2

Subsituindo:

int (sqrt(x^2 - 9))/(x^3) d x = int (sqrt(9 sec^2 (theta) - 9))/(27 sec^3 (theta)) 3 sec (theta) tan (theta) d theta

= int (sqrt(9 (sec^2 (theta) - 1)))/(9 sec^2 (theta)) tan (theta) d theta

Ta lembrado daquela propriedade trigonométrica: tan^2 (theta) + 1 = sec^2 ( theta ) ?!

Vamos usá-la, então, substituindo

int (sqrt(9 (sec^2 (theta) - 1)))/(9 sec^2 (theta)) tan (theta) d theta

= int (sqrt(9 tan^2 (theta)))/(9 sec^2 (theta)) tan (theta) d theta

= int (3 tan (theta))/(9 sec^2 (theta)) tan (theta) d theta

= int (tan^2 (theta))/(3 sec^2 (theta)) d theta

= (1)/(3) int sin^2 ( theta ) d theta

Passo 3

Vamos agora usar outra propriedade trigonométrica, que é a seguinte: sin^2 (theta) = (1)/(2) [1 - cos (2 theta)] .

Então, substituindo:

(1)/(3) int sin^2 (theta) d theta = (1)/(3) * (1)/(2) int (1 - cos (2 theta)) d theta

= (1)/(6) theta - (1)/(12) sin (2 theta) + c

= (1)/(6) theta - (1)/(6) sin (theta) cos (theta) + c

Lembra que dissemos que

x = 3 sec (theta)

Então

(x)/(3) = sec (theta) = (1)/(cos (theta))

Temos que

cos (theta) = (3)/(x)

Também podemos dizer que

theta = sec^(- 1) ((x)/(3))

Vimos que

sqrt(x^2 - 9) = 3 tan (theta)

Então

(sin (theta))/(cos (theta)) = (sqrt(x^2 - 9))/(3)

sin (theta) (x)/(3) = (sqrt(x^2 - 9))/(3)

Então podemos encontrar uma expressão para sin (theta)

sin (theta) = (sqrt(x^2 - 9))/(x)

Passo 4

Agora, que encontramos uma epressão para a theta , sin (theta) e cos (theta) podemos substituir

(1)/(6) theta - (1)/(6) sin (theta) cos (theta) + c = (1)/(6) sec^(- 1) ((x)/(3)) - (1)/(6) * (3)/(x) * (sqrt(x^2 - 9))/(x) + c

= (1)/(6) sec^(- 1) ((x)/(3)) - (sqrt(x^2 - 9))/(2 x^2) + c

Resposta

int (sqrt(x^2 - 9))/(x^3) d x = (1)/(6) sec^(- 1) ((x)/(3)) - (sqrt(x^2 - 9))/(2 x^2) + c

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

2. Seja f x uma função contínua. a) Mostre que a mudança de variável u = s e n ( x ) transforma a integral ∫ f s e n x ⋅ cos ⁡ x d x em ∫ f u d u
e) int (cos^3 ( x ))/(s e n^7 ( x )) d x
c) int (s e n (x))/(c o s^5 (x)) d x
d) int (s e n^3 (x))/(cos (x)) d x
b) int cos^3 (x) (1 + sqrt(s e n (x))) d x