Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 15.3 - Ex. 15
Calcule a integral dupla.
15.
é a região triangular com vértices e .
Passo 1
E aí, pessoal! Tudo beleza?
A questão quer o resultado da integral dupla na região triangular definida por vértices. Show, né?
Primeiramente vamos analisar a região ligando os vértices:
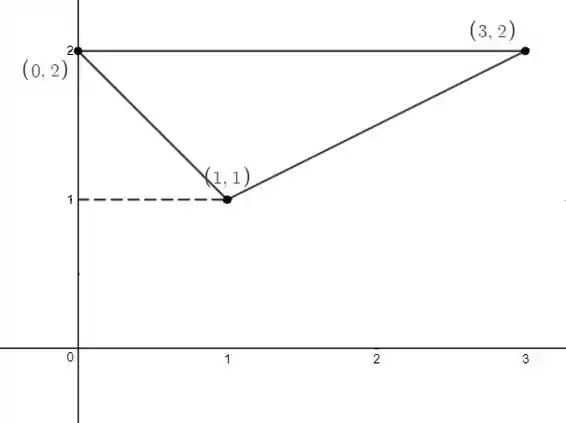
Para representar essa região como sendo do Tipo I (fazendo uma “sombra” em ) teríamos que dividir ela em duas, então, vamos representá-la como sendo do Tipo II (a “sombra” no eixo ).
Como escolhemos nosso tipo (que pode ser representada com uma seta na horizontal dentro da nossa região), no eixo temos bem definidos nossos limites de integração.
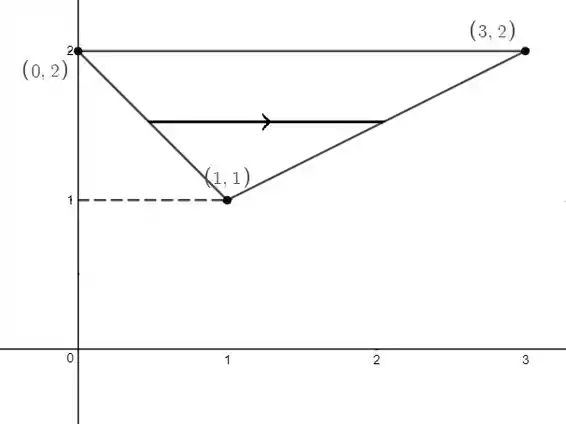
Já no eixo , a região não tem limites de integração bem definidas, pois estão entre duas retas.
Por isso, precisamos descobrir a inclinação das retas.
Passo 2
A inclinação é definida pela fórmula
A primeira reta passa por e , logo
E a reta é definida por
Isolando o
A outra reta passa por e , que tem inclinação
E a reta definida é
Isolando
Então podemos escrever os limites de integração da seguinte forma:
Passo 3
Agora vamos fazer a mágica acontecer.
Temos que
Observe que pela escolha do Tipo II, calculamos . Caso fosse do Tipo I, seria
Agora é só integrar, primeiro em relação a
Substituindo pelos limites de integração:
Agora integrando em relação a :
Colocando esse em evidência, podemos colocá-lo para fora da integral como uma constante.
Substituindo também pelos limites de integração,