Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diva Flemming - Cálculo B - Ed: 2º - Capítulo 7.6 - Ex. 17

17. Calcular ∬_R^() x d x d y , sendo R a região delimitada por y = - x , y = 4 x e y = (3)/(2) x + (5)/(2)

Passo 1

Temos que a representação gráfica é a seguinte:

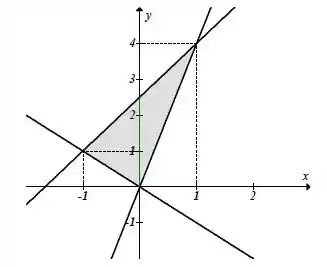
Analisando o gráfico, temos uma figura que não pode ser representada em apenas uma integral dupla, logo precisamos dividir em duas:

int_0^1 int_(- y)^((y)/(4)) x d x d y + int_1^4 int_((2)/(3) (y - (5)/(2)))^((y)/(4)) x d x d y

Vamos integrar em relação a x primeiro,

int_(- y)^((y)/(4)) x d x =

(((x^2)/(2))|_(- y)^((y)/(4)) = (y^2)/((16)/(2)) - (y^2)/(2) =

= (y^2)/(32) - (y^2)/(2)

Passo 2

int_0^1 ((y^2)/(32) - (y^2)/(2)) d y =

int_0^1 (- (15 y^2)/(32)) d y =

(- ((15 y^3)/(96))|_0^1 =

- (15)/(96) = - (5)/(32)

Passo 3

Agora iremos resolver o segundo termo:

int_1^4 int_((2)/(3) (y - (5)/(2)))^((y)/(4)) x d x d y

Vamos integrar em relação a x primeiro,

int_((2)/(3) (y - (5)/(2)))^((y)/(4)) x d x =

(((x^2)/(2))|_((2)/(3) (y - (5)/(2)))^((y)/(4)) = (y^2)/(32) - ((- 5 + 2 y)^2)/(18)

Passo 4

int_1^4 ((y^2)/(32) - ((- 5 + 2 y)^2)/(18)) d y =

int_1^4 ((y^2)/(32)) d y - int_1^4 (((- 5 + 2 y)^2)/(18)) d y =

Vamos resolver o primeiro termo e depois o segundo,

((y^3)/(96)|_1^4 = (21)/(32)

Agora o segundo termo,

- (1)/(18) int_1^4 (- 5 + 2 y)^2 d y =

- (1)/(18) int_1^4 (25 - 20 y + 4 y^2) d y =

(- (1)/(18) (25 y - 10 y^2 + (4 y^3)/(3))|_1^4 = - (1)/(18) (100 - 160 + (256)/(3) - 25 + 10 - (4)/(3))

= - (1)/(18) (- 75 + (252)/(3))

= - (1)/(18) (9)

= - (1)/(2)

Juntando os dois termos, temos que:

int_1^4 ((y^2)/(32)) d y - int_1^4 (((- 5 + 2 y)^2)/(18)) d y =

(21)/(32) - (1)/(2) = (5)/(32)

Passo 5

Ao juntar as integrais iniciais, temos:

- (5)/(32) + (5)/(32) = 0

Resposta

0

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule ∫ ∫ B y d x d y onde B é o conjunto dado.
Calcule ∫ ∫ B y d x d y onde B é o conjunto dado.
Calcule ∫ ∫ B f x ,y d x d y sendo dados:
Calcule ∫ ∫ B f x ,y d x d y sendo dados:
Calcule ∫ ∫ B f x ,y d x d y sendo dados: