Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Guidorizzi - Vol 3- Ed: 5º - Capítulo 3.1 - Ex. 6b

Calcule int_()^() int_B^() f (x , y) d x d y sendo dados:

Passo 1

Chamando a integral dupla do teorema de Fubini de F :

F = int_()^() int_B^() f (x , y) d x d y

Podemos reescrevê-la como:

F = int_()^() int_B^() x y d x d y

Ou:

F = int_a^b [int_(c (y))^(d (y)) x y d x] d y = int_c^d [int_(a (x))^(b (x)) x y d y] d x

Fazendo o esboço do conjunto B conclui-se que a figura é um círculo de raio r = sqrt(2) , mas devido às restrições das variáveis apenas uma região é a desejada. Então, desenhando essas restrições tem-se que a região amarela é a correta:

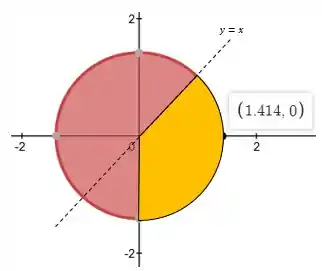
Só que vamos dividir em três partes:

Primeira:

0 <= x <= sqrt(2)

E

- sqrt(2 - x^2 ) <= y <= 0

Segunda:

0 <= x <= 1 (que é o ponto onde a reta encontra a circunferência)

E

0 <= y <= x

Terceira:

1 <= x <= sqrt(2)

E

0 <= y <= sqrt(2 - x^2)

Passo 2

Assim, é possível calcular:

F = int_0^(sqrt(2)) [int_(y = - sqrt(2 - x^2))^(y = 0) x y d y] d x + int_0^1 [int_(y = 0)^(y = x) x y d y] d x + int_1^(sqrt(2)) [int_(y = 0)^(y = sqrt(2 - x^2)) x y d y] d x

F = int_0^(sqrt(2)) x [(y^2)/(2)]_(y = - sqrt(2 - x^2))^(y = 0) d x + int_0^1 x [(y^2)/(2)]_(y = 0)^(y = x) d x + int_1^(sqrt(2)) x [(y^2)/(2)]_(y = 0)^(y = sqrt(2 - x^2)) d x

Substituindo o intervalo de integração em y :

F = int_0^(sqrt(2)) x [(0)/(2) - ((- sqrt(2 - x^2))^2)/(2)] d x + int_0^1 x [(x^2)/(2) - (0)/(2)] d x + int_1^(sqrt(2)) x [((sqrt(2 - x^2))^2)/(2) - (0)/(2)] d x

F = int_0^(sqrt(2)) x [(- 2 + x^2)/(2)] d x + int_0^1 x [(x^2)/(2)] d x + int_1^(sqrt(2)) x [(2 - x^2)/(2)] d x

F = int_0^(sqrt(2)) (- 2 x)/(2) + (x^3)/(2) d x + int_0^1 (x^3)/(2) d x + int_1^(sqrt(2)) (2 x)/(2) - (x^3)/(2) d x

F = int_0^(sqrt(2)) - x + (x^3)/(2) d x + int_0^1 (x^3)/(2) d x + int_1^(sqrt(2)) x - (x^3)/(2) d x

Passo 3

Agora, integrando em relação a x :

F = [- (x^2)/(2) + (x^4)/(4 . 2)]_0^(sqrt(2)) + [(x^4)/(4 . 2)]_0^1 + [(x^2)/(2) - (x^4)/(4 . 2)]_1^(sqrt(2))

F = (- ((sqrt(2))^2)/(2) + ((sqrt(2))^4)/(4 . 2)) - (- (0^2)/(2) + (0^4)/(4 . 2)) + ((1^4)/(4 . 2)) - ((0^4)/(4 . 2)) + (((sqrt(2))^2)/(2) - ((sqrt(2))^4)/(4 . 2)) - ((1^2)/(2) - (1^4)/(4 . 2))

F = - (2)/(2) + (4)/(8) + (1)/(8) + (2)/(2) - (4)/(8) - (1)/(2) + (1)/(8)

F = - 1 + (1)/(2) + (1)/(8) + 1 - (1)/(2) - (1)/(2) + (1)/(8)

F = (1)/(8) - (1)/(2) + (1)/(8)

F = - (2)/(8)

Show de bola! Conseguimos!

Resposta

- (2)/(8)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Nos Exercícios 9-18, escreva a integral iterada de ∬ R   d A sobre a região descrita R utilizando (a) seções transversais verticais, (b) seções transversais horizontais.
Minimizando uma integral dupla Que região R no plano x y minimiza o valor de ∬ R   x 2 + y 2 - 9 d A ? Justifique sua resposta.
Nos Exercícios 9-18, escreva a integral iterada de ∬ R   d A sobre a região descrita R utilizando (a) seções transversais verticais, (b) seções transversais horizontais.
Maximizando uma integral dupla Que região R no plano x y maximiza o valor de ∬ R   4 - x 2 - 2 y 2 d A ? Justifique sua resposta.
Nos Exercícios 9-18, escreva a integral iterada de ∬ R   d A sobre a região descrita R utilizando (a) seções transversais verticais, (b) seções transversais horizontais.