Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 15.Revisão - Ex. 20

Calcule o valor da integral múltipla.

∫ ∫ D y   d A

Onde D é a região do primeiro quadrante que está acima da hipérbole x y = 1 e da reta y = x e abaixo da reta y = 2 .

Passo 1

E aí meus queridxs, tudo bom com vocês? Vamos lá, precisamos calcular a integral acima de acordo com a região dada. Para isso, vamos primeiramente reescrever nossa integral de forma que ela possa ser escrita como uma integral iterada, então, tomemos a região de integração dada por: D é a região do primeiro quadrante que está acima da hipérbole x y = 1 e da reta y = x e abaixo da reta y = 2 . Nossa região de integração é dada por

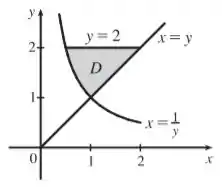
Assim, conseguiremos reescrever nossa integral como sendo

∫ 1 2 ∫ 1 y y y   d x   d y  

Passo 2

Beleza, agora que temos nossa integral escrita de forma iterada podemos calcular seu valor de forma bem tranquila, vindo de ‘dentro pra fora’ e enquanto resolvemos uma integral em uma variável consideraremos tudo o que não for essa variável como constante. Dessa forma, temos

∫ 1 2 ∫ 1 y y y   d x   d y  

Resolvendo a integral mais interna vamos ter

∫ 1 / y y y   d x   = x y 1 y y = y - 1 y ⋅ y

Agora, ficamos com a seguinte integral simples a ser resolvida

∫ 1 2 y - 1 y ⋅ y   d y = y 3 3 - y 1 2 = 8 3 - 2 - 1 3 + 1 = 4 3

Pronto, tá resolvido nosso exercício sem muitos problemas.

Resposta

4 3

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Transformando uma integral dupla para obter limites constantes Algumas vezes, uma integral multipla com limites variaveis pode ser mudada para uma com limites constantes. Mudando a ordem de integracao
a) Coordenadas polares Mostre, mudando para coordenadas polares, que ∫ 0 asin ⁡ β ∫ yc o t gβ a 2 - y 2 ln ⁡ x 2 + y 2 d x d y = a 2β ( ln ⁡ a - 1 2) Onde a0e0βπ 2 b) Reescreva a integral cartesiana c
Nos Exercícios 1-12, calcule a integral iteradaint_(pi)^(2 pi) int_0^(pi) ( s e n x + c o s y ) d x d y
Nos Exercícios 1-12, calcule a integral iteradaint_(- 1)^2 int_0^(pi // 2) y s e n x d x d y
É possível calcular a integral de uma função contínua f ( x , y ) sobre uma região retangular no plano x y e obter respostas diferentes dependendo da ordem de integração? Justifique sua resposta.