Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.7 - Ex. 47
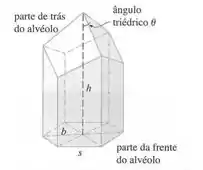
Em uma colmeia, cada alvéolo é um prisma hexagonal regular, aberto em uma extremidade com um ângulo triédrico na outra extremidade. Acredita-se que as abelhas formam esses alvéolos de modo a minimizar a área da superfície para um dado volume, usando assim uma quantidade mínima de cera na construção. O exame desses alvéolos mostrou que a medida do ângulo do ápice é surpreendentemente consistente. Baseado na geometria do alvéolo, pode ser mostrado que a área da superfície é dada por
onde , o comprimento dos lados do hexágono, e , a altura, são constantes.
- Calcule
- Que ângulo as abelhas deveriam preferir?
- Determine a área da superfície mínima do alvéolo (em termos de e ).
Observação: Medidas reais do ângulo em colmeias foram feitas, e as medidas desses ângulos raramente diferem do valor calculado em mais que .
Passo 1
Fala, galera! Beleza? Vamos resolver essa questão!
O enunciado nos deu a seguinte função:
Que representa a área da superfície de um alvéolo construído por abelhas. Segundo estudos, acredita-se que essa é a área que retem o maior volume usando o mínimo de cera em sua construção.
Teremos que calcular a derivada dessa função em relação a para encontrar um ângulo mínimo que as abelhas iriam preferir e determinar a área da superfície mínima do alvéolo em termos de e .
Então, basicamente, o que nós vamos fazer é derivar essa equação e igualar o resultado a zero para encontrar os pontos críticos e depois, substituir esses valores na equação da superfície .
Vamos lá!
Passo 2
Vamos começar calculando , derivando a nossa equação. Sendo
Sua derivada será calculada usando as derivadas tabeladas da cotangente e da cossecante. Assim:
Que pode ser reescrita na forma:
Maravilha.
Passo 3
(b) Agora para encontrar o ângulo igualamos a zero. Como a cossecante não pode assumir valor zero, podemos ver a parte
como uma constante e resolver apenas com o termo dentro dos parênteses:
Como
e
por definição, vamos ter então:
Assim,
E isolando o cosseno:
Analisando a tabela trigonométrica, o ângulo que possui esse cosseno mede .
Passo 4
(c) Como temos um
podemos achar na tabela trigonométrica do ângulo que
e que
Então, substituindo esses valores na equação que o enunciado nos deu, a área da superfície é:
Simplificando:
Valeu, galera! Até a próxima! 😉