Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 4.5 - Ex. 36
Um cone é feito de uma folha circular com raio recortando um setor e colando os lados que sobraram (Figura Ex-36). Qual é o máximo volume possível para o cone?
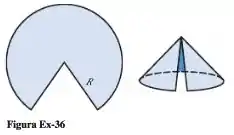
Passo 1
Então pessoal, vamos chamar a altura do cone de , o raio de e a altura inclinada de , assim como o enunciado propõe mesmo, tudo jóia? Show! O volume de um cone desse tipo é:
Para facilitar nossa visualização, temos o seguinte:
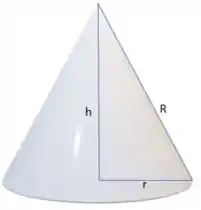
E do triângulo retângulo formando por , e temos:
Isolando , teremos:
Substituindo na expressão do volume:
Show! Como e são nossas variáveis, então tivemos que realizar essas substituição para eliminar uma das variáveis, ok? Então vamos continuar!
Passo 2
Como queremos o volume máximo, então vamos utilizar os conceitos do cálculo e derivar essa nossa função aí, saca só:
Igualando a zero:
A única forma disso dar zero é se:
Aqui vale ressaltar que não pegamos a raíz negativa porque não trabalhamos com coordenadas negativas na geometria, pois não faria muito sentido, não é mesmo?
Passo 3
Agora que encontramos , para encontrarmos o volume máximo é tranquilo, pois basta substituirmos o que encontramos na expressão do volume do passo 1, olha só:
E está aí nossa resolução, pessoal! 😉