Considere o sólido obtido pela rotação da região mostrada na figura em torno do eixo . Esboce uma casca cilíndrica típica e encontre sua circunferência e altura. Use cascas para encontrar o volume . Você acha que esse método é preferível ao fatiamento? Explique.
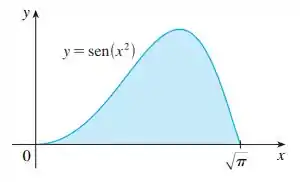
Passo 1
Opa, bora lá! Esboçando uma casca cilíndrica:
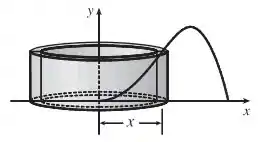
Uma típica casca cilíndrica tem uma circunferência valendo e altura .
Passo 2
Calculando seu volume:
Diremos que , e , então, substituindo temos
Passo 3
Pelo método de fatiamento, nós primeiro iríamos localizar o ponto de máximo local de usando os métodos do Capítulo 4, depois resolveríamos a equação para em termos de para obter as funções e como na figura abaixo
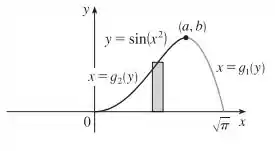
Finalmente, nós encontraríamos o volume usando . Usar as cascas nesse caso é bem mais fácil que usar o fatiamento.
Resposta
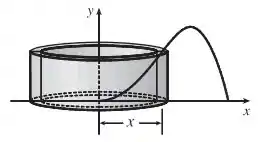
Uma típica casca cilíndrica tem uma circunferência valendo e altura .