Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 3.7 - Ex. 12

  1. Os critais de cloreto de sódio são fáceis de crescer no formato de cubo, ao se permitir uma solução de água e cloreto de sódio evaporar vagarosamente. Se V for o volume de cada cubo com comprimento de lado x , calcule d V / d x quando x = 3 m m e explique seu significado.
  2. Mostre que a taxa de variação do volume de cada cubo em relação ao comprimento da aresta é igual a metade da área da superfície do cubo. Explique geometricamente por que esse resultado é verdadeiro, mostrando um argumento análogo ao do Exercício 11(b).

Passo 1

Opa, bora resolver esse problema! Temos uma historinha aqui, o texto nos diz que os cristais de cloreto crecem formando cubos em determinadas condições.

Sabendo que V é o volume de cada cubo, podemos escrever o volume de um cubo como sendo:

V x = x 3

O enunciado pede pra a gente calcular d V / d x quando x = 3 m m :

d V d x = V ' x = 3 x 2

Substituindo:

V ' 3 = 3 ⋅ 3 2 = 27 m m 3 / m m

Isso significa que quando x = 3 m m o volume esta aumentando a medida que x aumenta!

Passo 2

Na letra (b) devemos provar que a taxa de variação do volume de cada cubo em relação ao comprimento x é igual a metade da área da superfície do cubo. Essa área pode ser calculada por:

A x = 6 × x 2 = 6 x

Uma vez que o cubo tem 6 faces. Temos:

A x 2 = 3 x 2 = V ' ( x )

Provadissímo!

Passo 3

Agora precisamos entender o significado do cálculo acima usando a geometria. Pra isso desenhamos o esqueminha:

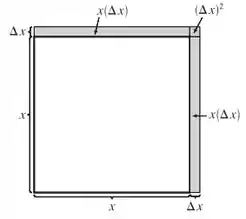
Podemos calcular a variação de volume fazendo:

∆ V = x 2 ∆ x + x 2 ∆ x + x 2 ∆ x + ∆ x 3

∆ V = 3 x 2 ∆ x + ∆ x 3

Agora vamos imaginar uma variação de comprimento muuuito pequena, ∆ x 3 ≈ 0 . Temos:

∆ V = 3 x 2 ∆ x

Daí,

∆ V ∆ x = 3 x 2

Chegamos no mesmo valor da derivada do volume! Ou seja, a derivada é nada mais nada menos do que a taxa de variação do volume =D.

Resposta

  1. V ' 3 = 27 m m 3 / m m
  2. A s x 2 = V ' x
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Quando uma bebida gelada e tirada da geladeira, sua temperatura é de 5 ° C. Depois de 25 minutos em uma sala a 20 ° C , sua temperatura terá aumentado para 10 ° C.(a) Qual é a temperatura da bebida de
O bismuto-210 rem uma meia vida de 5,0 dias.(a) Uma amostra tem originalmente uma massa de 800 mg. Encontre uma fórmula para a massa remanescente depois de t dias.(b) Encontre a massa remanescente dep
A tabela dá a população da Índia, em milhões, para a segunda metade do século X X .(a) Use o modelo exponencial e os valores do censo para 1951 e 1961 para prever a população em 2001 . Compare com o v
A tabela dá estimativas da população mundial, em milhões, de 1750 a 2000 .(a) Use o modelo exponencial e os valores da população para 1750 e 1800 para prever a população do mundo em 1900 e 1950 . Comp
(a) Quanto tempo levará para um investimento dobrar de valor se a taxa de juros for de 6 % , capitalizados continuamente?(b) Qual a taxa de juros anual equivalente?