Dada
Ache .
Passo 1
Nós poderíamos ver esse problema como um problema de módulo usar a definição de módulo e todo aquele blá blá blá, mas vamos dar uma simplificada e ver de uma forma mais gráfica. O gráfico de é:
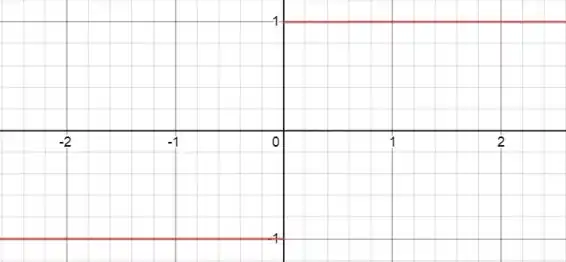
Passo 2
Para qualquer função, se temos uma mudança de parâmetro da forma é só transladarmos a função! Saca o gráfico da
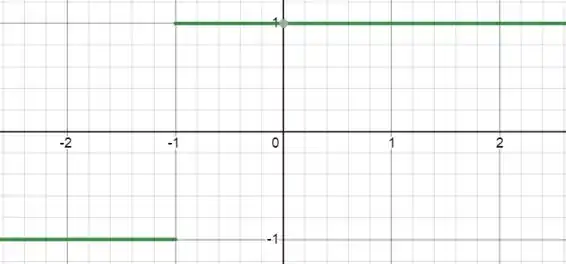
Percebe que é como se nós tivéssemos pegado a nossa e colocado ela mais a esquerda? É exatamente isso! Agora o eixo de simetria é no ponto ! Agora só nos resta escrever essa função analiticamente.
Passo 3
Sem stress né? Pelo gráfico, vemos que:
Quase pronto! Agora precisamos incluir o valor de na nova função. Se na nossa função original, , o mesmo vai acontecer na função transladada, porém no novo ponto de simetria! Então ficaremos com a função: