Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 3.2 - Ex. 4
Derive a função:
Passo 1
E aí! pessoal! 😬
Bom, galera... precisamos derivar a função
Mas neste caso a função é composta por uma multiplicação, então o que fazemos?
Usamos a Regra do Produto!
Então:
Veja só! 😉
Passo 2
Vamos relembrar da Regra da Potência:
Para finalizar usamos a Derivada para a função exponencial:
Sendo assim:
Agora vamos colocar tudo em uma única fração:
Tirando o Mínimo Múltiplo Comum:
Para isso nós multiplicamos o que não é fração ainda, pelo denominador que está embaixo do 1, isso em cima e em baixo, assim:
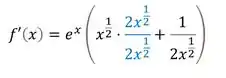
Vamos agora multiplicar por na parte de cima, e como são potencias de bases iguais, nós repetimos a base que é e somamos os expoentes, ficando com:
Assim:
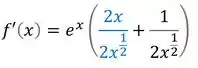
E como as duas frações possuem agora o mesmo denominador, podemos colocar tudo junto, assim:
Isolando:
E então! O que achou? Responde Aí! 😉
