Enunciado
Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 1.1 - Ex. 2
Desenhe um campo de direções para equação diferencial dada. Baseado no campo de direções, determine o comportamento de y quanto Se esse comportamento depender do valor inicial de em , descreva essa dependência.
Passo 1
Vamos lá! Temos uma diferencial da seguinte forma:
O problema ta pedindo pra a gente desenhar um campo de direções, e aqui a gente vai ver qual é o comportamento da função sem precisar resolver a EDO!
A dica que a gente recebe no enunciado é que a função é do tipo , mas o não aparece na EDO.
Então a gente vai fazer o seguinte, vamos substituir vários valores para , descobrir e montar nosso campo de direções.
Começando por :
Para
Mas a gente tem que fazer isso com váaaarios pontos, então eu vou deixar uma tabelinha com o resultado!
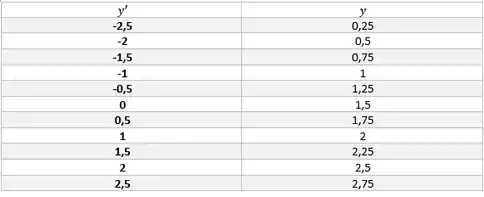
Passo 2
E como a gente transforma essa tabela em um campo de direções?!
Vamos lá! é a derivada, certo? Então ela diz da pra a gente a inclinação da reta no ponto correspondente!
Por exemplo, para a gente tem , então a gente vai em e desenhamos uma reta pequenininha com inclinação negativa de .
Em temos , isso significa que vamos desenhar a mesma reta pequenininha, mas dessa vez ela vai ter inclinação positiva!
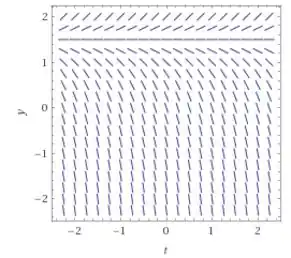
Olhando o campo de direções a gente ve que a medida que nos aproximamos de a inclinação vai diminuindo e divergem em que é como se as retinhas estivessem saindo da inclinação de e se “abrindo”!
Como o não aparece na derivada então a inclinação da reta vai ser igual para qualquer valor de , então quando , o comportamento das inclinações da reta continuam iguais!
Resposta
Ei, a resposta está no passo a passo :)