Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 15.2 - Ex. 32
Desenhe o sólido que está entre a superfície e o plano e é limitado pelos planos e . A seguir, determine seu volume.
Passo 1
Faaaaala meu povo!! Tudo na paz!? Bora resolver mais uma.
Avaliando o enunciado, nossa primeira missão é desenhar o sólido. Sendo que ele está entre a superfície e o plano e é limitado pelos planos e . Depois, devemos determinar seu volume.
E agora?
Para fazer o desenho do sólido, vamos utilizar algum software. Porque? Principalmente devido a superfície, pois seu gráfico é complicado de fazer a mão.
Já o plano é mais fácil, conseguimos fazer adotando primeiro , aí vamos ficar com a reta . E depois fazendo , vamos ficar com outra reta, porém . Feito isso, esboçamos no tridimensional.
Para o volume, lembre-se da fórmula geral:
Onde, é a função que delimita a região, e é nossa região de integração, que nesse caso vai ser delimitado pelos planos.
Nesse caso, z(x,y) é a superfície que esta acima menos a superfície que esta abaixo, por isso é importante o esboço das regiões.
Observe a variação de e , temos que:
Passo 2
Pessoal, pra ter uma ideia do desenho do sólido, vamos desenhar primeiro as duas superfícies que o limitam em .
Para o plano .
Vamos adotar primeiro, logo ficamos com a reta:
Plotando vamos ter:
Agora vamos adotar primeiro, logo ficamos com a reta:
Plotando vamos ter:
Com esses gráficos temos uma ideia de como vai ser o comportar em três dimensões.
Passo 3
Plotando em três dimensões vamos ter:
Em azul, o plano ;
Em roxo, a superfície ;
Observando o gráfico abaixo, podemos ver que nossa região está entre as duas curvas. Mas lembre-se que ela tem limitações com planos em e também. Sendo elas:
Essas informações são essenciais para montar nossa integral.
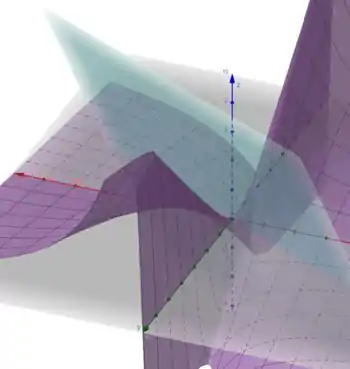
Passo 4
Pra determinar o volume desse sólido, primeiro precisamos escrever uma integral dupla que o descreva. Sabemos que:
Olhando para os planos, temos que os limites de integração são:
Logo,
Obtemos a partir da equação das superfícies desenhadas no passo anterior. Pelo desenho, temos que o plano delimita por cima, então:
Então, escrevemos a integral assim:
Passo 5
Quando a gente tem uma integral dupla, a gente sempre começa resolvendo de dentro pra fora, assim:
Integrando em , vamos ter:
Aplicando os limites de integração:
Passo 6
Agora, é só resolver a integral simples que restou:
Integrando em :
Aplicando os limites de integração:
Logo, o volume é: