Determinar se possível a área da região sob o gráfico da função de .
Passo 1
Querem saber área que está debaixo dessa curva aqui:
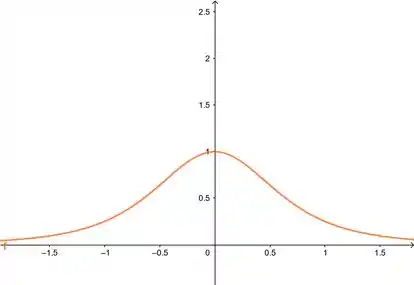
Passo 2
Pra isso, a gente precisa calcular (se possível) a integral:
Vamos calcular a integral indefinida primeiro:
Pra calcular essa a gente pode usar uma substituição trigonométrica, podemos fazer .
Daí teremos e .
Aí vai ficar:
Passo 3
Beleza, vamos voltar para a variável agora.
A gente tem que:
Agora a gente volta pro resultado:
Como essa é uma função par, podemos analisar só o caso em que os valores são positivos e no final dobramos o valor.
Passo 4
Vamos lá, a área vai ser dada por:
Aí a gente jogar pro limite:
Então a área pedida é:
Prontinho! Área calculada😉