Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 15.Revisão - Ex. 39

Determine a área da parte da superfície z = x 2 + y que está acima do triângulo com vértices 0,0 , 1,0 e 0,2 .

Passo 1

Vamos lá galerinha, tudo certo? Temos que encontrar uma área de uma superfície acima de uma área qualquer, nesse caso temos a função z que representa a altura em cada ponto

z = x 2 + y

Sendo que a área abaixo desses pontos é o seguinte triângulo

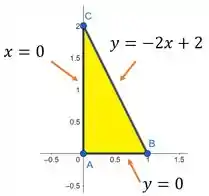
Muito cuidado meu amigo. Não é a área do triangulo que queremos, é a área da função z definida nesses limites. Então nosso primeiro passo é lembrar primeiramente como calculamos a área de uma superfície. Para isto, basta resolver a seguinte integral:

A S = ∬ D 1 + ∂ z ∂ x 2 + ∂ z ∂ y 2 d A

Portanto, precisamos calcular primeiramente as derivadas parciais de z em função de x e de y para só depois resolvermos as integrais, definir e identificar os limites de integração.

Passo 2

Vamos determinar primeiramente as derivadas parciais da função z = f x , y . Sendo assim

∂ z ∂ x = 2 x

∂ z ∂ y = 1

Portanto, devemos resolver a seguinte integral:

A S = ∬ D 1 + 2 x 2 + 1 2 d A = ∬ D 2 + 4 x 2 d A

Passo 3

A nossa região pode ser visualizada abaixo:

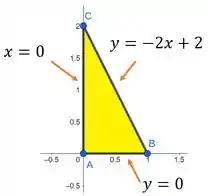
A região pode ser descrita como tanto do tipo I quanto do tipo II. Lembrando que uma região do tipo I é uma região que será “varrida” pela integral no sentido vertical entre duas funções de y . Enquanto que tipo II é definida no sentido horizontal por funções de x .

Devido à presença de uma função de x ao quadrado dentro da raiz, a integral se torna mais fácil de ser resolvida se descrevermos a região como sendo do tipo I (Ou seja, escreveremos y em função de x ). Portanto,

0 ≤ x ≤ 1

0 ≤ y ≤ - 2 x + 2

Passo 4

Agora, só nos basta aplicarmos os limites de integração e resolvermos a integral. Portanto,

A S = ∫ 0 1 ∫ 0 - 2 x + 2 2 + 4 x 2 d y d x

Integrando em relação a y   e aplicando os limites de integração:

A S = ∫ 0 1 2 + 4 x 2 ⋅ y 0 - 2 x + 2 d x = ∫ 0 1 ( - 2 x + 2 ) 2 + 4 x 2 d x

Podemos separar em duas integrais, vamos chamar a da esquerda de A e a da direita de B .

A S = ∫ 0 1 - 2 x 2 + 4 x 2 d x + ∫ 0 1 2 2 + 4 x 2 d x

A integral B é uma integral primordial do tipo:

∫ a 2 + u 2   d u  

Que é tabelada com o seguinte resultado:

u 2 a 2 + u 2 + a 2 2 ln ⁡ u + a 2 + u 2

Aplicando à nossa integral teremos:

2 x 2 2 + 4 x 2 + 2 2 ln ⁡ 2 x + 2 + 4 x 2 0 1

Simplificando e aplicando os limites temos:

6 + ln ⁡ 2 + 2 + 4 -   ln ⁡ 2

Vamos resolver agora a integral A por substituição:

∫ 0 1 - 2 x 2 + 4 x 2 d x

u = 2 + 4 x 2 ;       d u = 8 x   d x

Então temos:

∫ 0 1 - 2 x 2 + 4 x 2 d x =   ∫ 0 1 - 2 x 8 x u   d u

Simplificando e integrando:

2 8 ∫ u 1 2   d u = 2 12   u 3 2  

Retornando para x e aplicando os limites de integração:

1 6 2 + 4 x 2 3 2 0 1 =   1 6 6 3 2 - 2 3 2  

Resolvendo subtração das integrais:

6 + ln ⁡ 2 + 6 -   ln ⁡ 2 -   1 6 6 3 2 + 1 6 2 3 2

Simplificando e colocando os valores temos:

2,449 + 1,492 - 0,346 -   2,449 + 0,471 = 1,617

Resposta

6 + ln ⁡ 2 + 6 -   ln ⁡ 2 -   1 6 6 3 2 + 1 6 2 3 2 = 1,617

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Esboce o sólido cujo volume é dado pela integral iterada. ∫ 0 1 ∫ 0 1 - x 2 1 - xd yd x
Use um sistema de computação algébrico para determinar o volume exato do sólido.Abaixo da superfície z = x 3 y 4 + x y 2 e acima da região limitada pelas curvas y = x 3 - x e y = x 2 + x para x ≥ 0 .
Calcule ∬ D 1 - x 2 - y 2 d A , onde D é o disco x 2 + y 2 ≤ 1 , identificando primeiro a integral como o volume de um sólido.
Desenhe o sólido limitado pelo plano x + y + z = 1 e pelo paraboloide z = 4 - x 2 - y 2 e determine seu volume exato. (Utilize seu SCA para fazer esse desenho, para achar as equações das fronteiras da
Utilize coordenadas polares para determinar o volume do sólido dado.Dentro da esfera x 2 + y 2 + z 2 = 16 e fora do cilindro x 2 + y 2 = 4 .