Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.4 - Ex. 12
Determine o centro de massa da lâmina do Exercício se a densidade em qualquer ponto for proporcional ao quadrado da distância do ponto à origem.
Passo 1
Faaala turminha, tudo na paz? Bora lá começar!!!
Esse exercício se baseia no enunciado da questão . Então vamos recapitular o que essa questão pedia:
Tínhamos um disco cuja a expressão é , e ele ocupa o primeiro quadrante.
O que muda do exercício 11 para esse, é que devemos considerar a densidade em qualquer ponto proporcional ao quadrado da distância do ponto ao a origem.
Vish, parece complicado isso? Calma, não é tão difícil assim.
Nosso primeiro passo é fazer um esboço desse disco no primeiro quadrante e achar essa distância da origem a um ponto qualquer no disco. Olha só como fica:
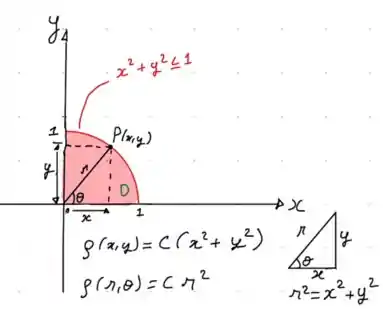
Assim, temos a densidade escrita como:
Essa constante escrevemos de forma genérica, ela pode assumir qualquer valor maior que zero, inclusive . Não se preocupe com ela, no fim você vai ver que o centro de massa não depende dela.
Precisamos lembrar das relações de coordenadas polares, que são as seguintes:
Sabemos que a massa e os centro de massas , são obtidos através das seguintes fórmulas:
A região , é nosso disco no primeiro quadrante. Que tem as seguintes parametrizações em coordenadas polares:
Agora é só você começar a calcular! Comece determinando a massa e depois encontre o centro de massa!
Bora lá!
Passo 2
Vamos começar determinando nossa densidade, pois ela é crucial na determinação da massa.
Como vimos no passo , ao esboçar nossa região conseguimos achar uma expressão para a densidade em função das coordenadas polares. Que é:
Sabendo disso, podemos calcular a massa:
Nossa região , também vimos que em coordenadas polares ela é escrita como:
Como é um círculo de raio igual , sabemos que varia de até . Já para o ângulo, sabemos que está no primeiro quadrante, logo o ângulo só pode variar entre e .
Com essas informações, vamos substituir na integral. Ficamos com:
Lembrando que em coordenadas polares é:
Assim temos que:
Passo 3
Bom, agora vamos integrar. Lembre-se que começamos de dentro para fora, e tudo que não depende da variável de integração consideramos como constante.
Assim, integrando em temos:
Aplicando os limites de integração, temos:
Agora vamos integrar em . Integrando ficamos com:
Aplicando os limites, temos que:
Assim, concluímos que a massa é:
Passo 4
Agora vamos determinar os centros de massa:
Lembrando que:
Vamos começar por . Substituindo os valores temos que:
Simplificando um pouco, temos:
Integrando em primeiro. Vamos ter:
Aplicando os limites de integração, temos:
Integrando em , temos:
Aplicando os limites de integração, vamos ter:
Logo, o centro de massa em relação a é:
Passo 5
Agora precisamos determinar o centro de massa em relação a .
O processo vai ser o mesmo que fizemos para .
Substituindo os valores em , vamos ter:
Simplificando, vamos ter:
Integrando primeiro em , vamos ter:
Aplicando os limites de integração, ficamos com:
Integrando em , temos que:
Aplicando os limites, ficamos com:
Logo, o centro de massa em relação a é:
Então, a posição do centro de massa é: