Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 15.Revisão - Ex. 34

Determine o volume do sólido dado. Acima do paraboloide z = x 2 + y 2 e abaixo do semicone z = x 2 + y 2 .

Passo 1

Faaaala pessoal, tudo bom? Bora lá

Temos que determinar o volume de um solido que está acima do paraboloide z = x 2 + y 2 e abaixo do semicone z = x 2 + y 2 .

Por onde começamos?

Uma dica: sempre que trabalhamos com sólidos que envolvem círculos, é mais fácil trabalharmos em coordenadas polares:

x 2 + y 2 = r 2

x = r c o s   θ

y = r s e n   θ

d x d y = r d r d θ

Queremos calcular o volume, certo? Lembra que volume é:

V = ∭ E d V

Onde, d V = d x d y d z e E é região do sólido.

Vamos pesar na nossa região E . Já sabemos que esta acima do paraboloide e abaixo do cone, pois foi dado no enunciado.

Primeiramente devemos encontrar onde nosso paraboloide se cruza com o semicone, e esse encontro ocorre em:

x 2 + y 2 = x 2 + y 2

Isso ocorre quando x 2 + y 2 = 1   o u   0 . Tendo uma equação com essa cara:

x 2 + y 2 = r 2

Sendo assim, nós teremos que o raio varia de:

0 ≤ r ≤ 1

Já o ângulo varia de:

0 ≤ θ ≤ 2 π

Já no eixo z , temos a variação de:

x 2 + y 2 ≤ z ≤ x 2 + y 2

Com essas informações em mãos, agora é montar a integral. Lembre-se de colocar tudo em coordenadas polares, e que sempre começamos integrando por limites que possui funções.

Bora lá!!!

Passo 2

Vamos começar recordando quem é nossa região de integração.

Quero primeiro que vocês observem o gráfico a seguir feito no Geogebra:

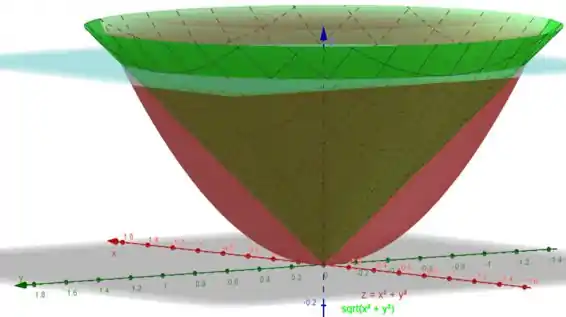
Observe que bate exatamente com o que falamos no passo 1. Temos o cone em verde e em vermelho o paraboloide. Perceba que eles se encontram em z = 0 e z = 1 (onde está o plano em azul).

Logo na intersecção das duas, temos o círculo:

x 2 + y 2 ≤ 1

Assim, temos que determinar a seguinte integral de volume:

V = ∭ E d V

Onde, d V = d x d y d z e E é região do sólido.

Sabemos do passo 1 que nossos intervalos de integração é:

0 ≤ r ≤ 1

0 ≤ θ ≤ 2 π

x 2 + y 2 ≤ z ≤ x 2 + y 2

Mas queremos trabalhar tudo em coordenadas polares. Então vamos substituir os valores de x e y por:

x = r c o s   θ

y = r s e n   θ

d x d y = r d r d θ

Agora, é só montar a integral. Lembrando que devemos começar integrando de dentro para fora, e a integral de dentro sempre começa pelos limites de integração com função.

Dessa forma, nossa integral vai ficar:

V = ∫ ∫ x 2 + y 2 ≤ 1 ∫ x 2 + y 2 x 2 + y 2 d z   d x d y

Em coordenadas polares:

V = ∫ 0 2 π ∫ 0 1 ∫ r 2 r r   d z   d r   d θ

Passo 3

Nossa missão agora é integrar. Vamos começar integrando em d z .

Integrando temos que:

V = ∫ 0 2 π ∫ 0 1 r   z r 2 r   d r   d θ

Aplicando os limites de integração, temos:

V = ∫ 0 2 π ∫ 0 1 r 2 - r 3   d r   d θ

Agora, vamos integrar em d r . Integrando, ficamos com:

V = ∫ 0 2 π r 3 3 - r 4 4 0 1   d θ

Aplicando novamente os limites de integração, temos:

V = ∫ 0 2 π 1 12   d θ = 2 π 12 = π 6

Por fim, restou uma integral simples em d θ . Integrando vamos ter:

V = 1 12 θ 0 2 π

Aplicando os limites de integração, temos:

V = 1 12 ( 2 π )

Logo nossa resposta é:

V = π 6

Resposta

V = π 6

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Use a integral tripla para determinar o volume do sólido dado.O sólido delimitado pelo cilindro elíptico 4 x 2 + z 2 = 4 e pelos planos y = 0 e y = z + 2
Use a integral tripla para determinar o volume do sólido dado.O sólido limitado pelo paraboloide x = y 2 + z 2 e pelo plano x = 16
Use a integral tripla para determinar o volume do sólido dado.O sólido delimitado pelo cilindro x = y 2 e pelos planos z = 0 e x + z = 1
Use a integral tripla para determinar o volume do sólido dado.O tetraedro limitado pelos planos coordenados e pelo plano 2 x + y + z = 4 .
Calcule a integral tripla. ∭ E x yd V , onde E é delimitado pelo cilindro parabólico y = x 2 e x = y 2 e pelos planos z = 0 e z = x + y