Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 15.3 - Ex. 26
Determine o volume do sólido dado.
26.
Delimitado pelo paraboloide e pelos planos , , ,
Passo 1
Fala, galera!
O enunciado pede pra determinar o volume do sólido delimitado por uma paraboloide e por planos. Moleza?
Que sólido é esse?? Bom, pelas equações que temos, iremos descobrir.
O volume é definido por três eixos (, certo?
Uma função pode ser representada como . Opa! Temos a nossa fórmula do paraboloide ali bem parecido.
Como , então encontramos nossa função no plano :
Passo 2
Para encontrar nossos limites de integração, presta atenção aqui!
Podemos representar como sendo uma região dos dois tipos, ou seja, tem “sombra” tanto no eixo quanto no .
Temos que, para o plano , basta que analizemos a região delimitada pelos outros planos e calcular a integral normalmente.
Olhando para as equações , e no plano, temos:
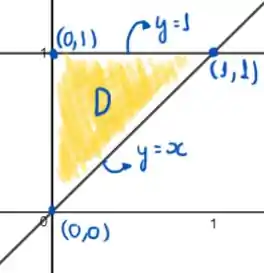
Pela análise do gráfico, podemos escrever da seguinte forma
Passo 3
Temos então que o volume do solido que é restrito abaixo de na região é dado por
Agora vamos resolver a integral de dentro, em relação a :
Substituindo os limites de integração:
Show! Agora vamos integrar em relação a
Substituindo os limites de integração aqui também: