Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.7 - Ex. 24
Use coordenadas cilíndricas.
Determine o volume do sólido que está entre o paraboloide e a esfera .
Passo 1
Fala, gente bonita. Tudo certinho?
Olha só, a questão quer que a gente use coordenadas cilíndricas para descobrir o volume do sólido que está entre esse paraboloide:
E entre essa esfera aqui, ó:
Aqui está a região que estamos calculando:
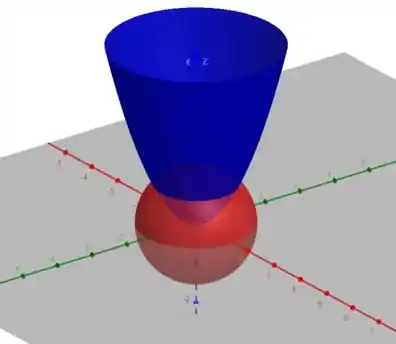
Vamos começar relembrando alguns termos das coordenadas cilíndricas antes de começar a encontrar os limites de integração?
Aqui estão:
Show de bolinha! 😊
Passo 2
O sólido está limitado acima pela esfera e abaixo pelo paraboloide. Então para o volume temos essa formulinha aqui, olha só:
Para nossa região , vamos analisar o que já temos.
No paraboloide
Então
E pela esfera, sabemos que:
Descobrimos a região no eixo .
Para os dois sólidos, podemos igualar o valor de das duas equações (paraboloide e esfera). Portanto, temos:
Passando para coordenadas polares, temos:
Colocando termos em evidência:
Como e pertence aos números reais, a única solução se dá quando:
E pelo gráfico, vemos que temos uma região positiva acima do eixo . Assim:
Passo 3
Montando nossa integral:
Resolveremos primeiro de dentro para fora. Ou seja, primeiro em relação a :
Substituindo pelos limites de Integración...
Multiplicando pelo de fora:
Agora em relação a :
Resolvendo, teremos:
Fazendo o m.m.c. com os denominadores:
Agora em relação a :
Colocando para fora, como constante:
Assim:
Show de bola! 😉