Enunciado
Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 2.1 - Ex. 18f
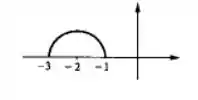
Dê o domínio e esboce o gráfico.
Passo 1
Olá, tudo bem? Antes de tudo, vou começar determinando a equação implícita:
Elevando os dois lados ao quadrado:
E trazendo para o lado esquerdo temos:
Ah! Saca só porque eu comecei fazendo isso: essa equação se parece com o que? Não é do tipo:
É sim! E essa é a equação de uma circunferência na sua forma reduzida =D
Os valores de e fornecem o centro do círculo e o é o raio. No nosso caso esse círculo está centrado em e tem raio . Como a função original é com a raiz positiva, então sabemos que queremos apenas a parte superior do círculo!
Passo 2
Beleza até aqui? Bom, agora que já sabemos o centro e o raio, ficou tranquilo de fazer o esboço do gráfico. Se você não lembra de alguma parte, não fica triste não! O Responde Aí tá aqui pra te ajudar! Dá uma espiadinha na parte de circunferência na nossa plataforma e retorna aqui!!
E o domínio? Bom, essa função não pode fornecer valores inválidos de , então temos que o radicando deve ser sempre maior ou igual a zero:
Vamos analisar onde essa função é zero: .
Essa é uma equação de segunda ordem com e vamos analisar seu sinal. Pela fórmula de Bhaskara temos:
Então os valores que satisfazem essa equação são: e . Entre esses valores a função assume valores negativos, que é a região de interesse.
Então os valores que satisfazem essa inequação são: . E o domínio pode ser escrito dessa forma:
Passo 3
Vamos ao esboço? Lemrbando que queremos a parte de cima da circunferência de raio e centro temos:
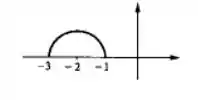
Beleza? Vamos pra próxima?
Resposta
