Encontre a área do maior retângulo que pode ser inscrito na elipse
Passo 1
Oii pessoal, show de bola??
“A loucura é como a gravidade, só precisa de um empurrãozinhooo...”

Bora empurrar e macetar essa questãozinha comigo agora
A questão pede para encontrar a área do maior retângulo que pode ser desenhado dentro de uma elipse, ou seja, um retângulo cujos vértices tocam a elipse em pontos distintos.
A equação da elipse é dada como
onde são os comprimentos dos semi-eixos maior e menor da elipse, respectivamente.
Nós sabemos que a área do retângulo é dada pelo produto da base pela altura.
Se chamarmos a base de e a altura de , teremos:
E nós queremos que essa área seja máxima.
Então, o que nós vamos fazer é isolar uma das variáveis na equação da elipse e substituir na equação de área do retângulo.
Depois, vamos encontrar os pontos de máximo dessa função, derivando e igualando a zero para obter os pontos críticos e avaliando eles dentro da função.
Passo 2
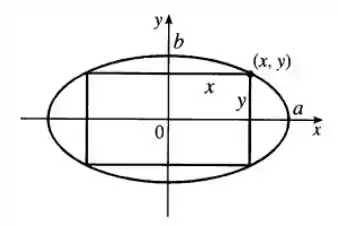
Para encontrar o maior retângulo possível dentro da elipse, precisamos considerar um retângulo cujos lados são paralelos aos eixos coordenados.
Vamos usar a simetria da elipse e a geometria analítica para nos ajudar.
Coordenadas dos Vértices do Retângulo
Os vértices do retângulo serão
Esses pontos precisam estar na elipse, portanto, devem satisfazer a equação da elipse
Uso de Multiplicadores de Lagrange
Para encontrar os pontos que maximizam usamos o método dos multiplicadores de Lagrange.
Consideramos a função objetivo e a restrição
Passo 3
Formulando o Problema com Lagrange
Definimos a função de Lagrange:
Calculamos as derivadas parciais e igualamos a zero:
Passo 4
Resolvido o Sistema de Equações
Das duas primeiras equações, resolvemos \(\lambda\):
Multiplicamos ambos os lados por
Escolhemos a solução positiva:
Passo 5
Substituímos
na equação da elipse:
Passo 6
Então,
Calculando a Área Máxima
Finalmente, a área máxima do retângulo é:
Portanto, a área do maior retângulo que pode ser inscrito na elipse é
“Faça seus medos terem medo de você”

Resposta
Portanto, a área do maior retângulo que pode ser inscrito na elipse é