Encontre a área da região dentro de um laco, onde .
Passo 1
Faaalaaeee, beleza??
Bom... a questão foi bem direta... queremos calcular a área dentro de um laço da seguinte curva:
Mas que laço é esse???
O nosso gráfico parece uma flor. E esse “laço” que a questão menciona é como se fosse uma das pétalas, veja:
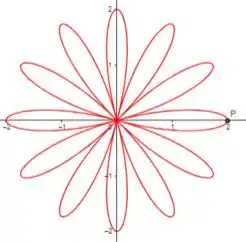
Mas e pra calcular a área? Como fazemos??
Bom... em coordenadas polares temos que a área de uma região é dada pela integral onde e a função que determina como o raio da curva varia em relação ao ângulo no intervalo .
No problema, precisamos identificar o intervalo onde a curva faz um laço, como a função que determina o raio e periódica de período menor que em algum momento ela “se fecha” e esse intervalo sera nosso domínio de integração.
Agora bora lá!! 😉
Passo 2
Bom... pela nossa figura, percebemos que a gente pode definir o limite inicial de integração em pois o valor de é zero nesse ângulo (ou seja, é o início do laço), tornando nossa continha mais simples.
Para fechar o intervalo de um laço, a gente soma o nosso com , veja:
Perceba que quando , o nosso também é zero.
Então temos um dos intervalos possíveis para um laço: .
Passo 3
Como a expressão do raio foi dada, já podemos calcular a integral:
Precisamos de uma substituição para resolver essa integral, vamos lá:
Usando as relações:
E a fórmula do arco duplo do cosseno:
Trocando por , passando o seno ao quadrado para o outro lado, substituindo e simplificando, temos:
Passo 4
Agora, substituindo a expressão na integral e resolvendo:
Simplificando o , temos:
Usando que uma primitiva da função na segunda integral é , temos
Resposta
Logo, a resposta sera .