Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.4 - Ex. 25
Encontre a área da região que está dentro da primeira curva e fora da segunda curva.
25. ,
Passo 1
Olá, meu nobre amigo. A gente aqui hoje vai calcular a área.
A gente tem as curvas:
E precisamos então encontrar a área da região que está dentro da primeira curva e fora da segunda curva.
Veja que estamos trabalhando aqui com coordenadas polares, e a área para coordenadas polares é dada por:
Passo 2
Agora vamos visualizar as duas curvas no plano polar, e montar a estratégia de resolução. Vamos utilizar aqui um software matemática para esboçar essa curva, estarei utilizando o GeoGebra.
Precisamos encontrar a região que está dentro da curva vermelha e fora da curva azul na imagem abaixo:
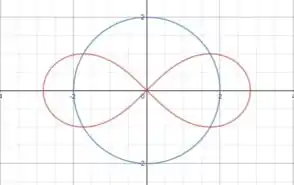
Essa região aqui:
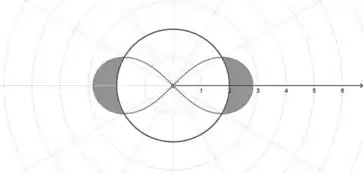
Para encontrarmos o intervalo do ângulo, nosso limite de integração, vamos igualar as duas equações:
Que corresponde ao valor de para os dois pontos de interseção no lado direito da figura acima, como ela é simétrica em relação aos dois eixos, podemos integrar no intervalo e multiplicar a integral por quatro.
Veja que se a gente calcular a área da figura do ‘loop’, e excluirmos a área do círculo, é exatamente o que a gente precisa. Então a gente vai fazer justamente isso.
E a integral da área:
Onde e .
Passo 3
Vamos então resolver nossa integral, lembre-se que iremos multiplicar por :
Realizando a integração: