Encontre o centroide da região.
O triângulo de vértices , e .
Passo 1
Temos esse carinha aqui:
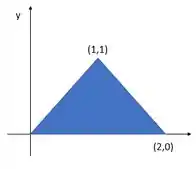
A ideia aqui é encontrar o centroide usando nossa fórmulinha:
Passo 2
Vamos tentar achar os limitantes dessa região no eixo e no eixo .
Em :
Mas temos duas retas nesse intervalo: em precisamos achar a reta que passa por e .
Em , precisamos achar a reta que passa por e . Ela tem essa cara:
Resolvendo o sisteminha:
Passo 3
Vamos achar as coordenadas do centroide por integração. Primeiro a coordenada :
Para , no eixo , nossa região está entre (por cima) e (por baixo). Já para para , no eixo , nossa região está entre (por cima) e (por baixo). Por isso vamos ter duas integrais, uma para cada intervalo.
Como temos um triângulo de altura e base :
Nossa integral fica:
Fazendo a distributiva e calculando a integral de polinômios:
A gente até já esperava esse valor, porque nosso triângulo é simétrico ao eixo vertical que passa por essa coordenada.
Passo 4
Agora a coordenada :
Elevando a função ao quadrado e calculando a integral de polinômios que aparecer: