Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 6.7 - Ex. 9

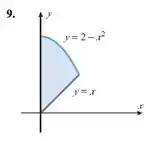
Encontre o centroide da região.

Passo 1

A ideia aqui é encontrar o centroide usando nossa fórmulinha:

overset(-)(x) = (1)/(á r e a d e R) int_a^b x ( f (x) - g (x) ) d x

overset(-)(y) = (1)/(á r e a d e R) int_a^b (1)/(2) [(f (x))^2 - (g (x))^2] d x

Passo 2

Vamos achar as coordenadas do centroide por integração. Primeiro a coordenada overset(-)(x) :

overset(-)(x) = (1)/(á r e a d e R) int_a^b x ( f (x) - g (x) ) d x

Para achar os limitantes da região no eixo x , precisamos fazer a intercessão entre curvas:

y = 2 - x^2 , y = x :. 2 - x^2 = x

Resolvendo a equação:

x = - 2 , x = 1

Mas, inferiormente, nosso x está visivelmente limitado em 0 , por isso no eixo x nossa região está entre 0 e 1 , e no eixo y , nossa região está entre y = f (x) = 2 - x^2 (por cima) e y = g (x) = x (por baixo).

A área pode ser calculada pela integral:

á r e a d e R = int_0^1 2 - x^2 - x d x = (7)/(6)

Nossa integral fica:

overset(-)(x) = (6)/(7) int_0^1 x (2 - x^2 - x) d x

Fazendo a distributiva e calculando a integral dos polinômios:

overset(-)(x) = (5)/(14)

Passo 3

Agora a coordenada overset(-)(y) :

overset(-)(y) = (1)/(á r e a d e R) int_a^b (1)/(2) [(f (x))^2 - (g (x))^2] d x

overset(-)(y) = (6)/(7) int_0^1 (1)/(2) ((2 - x^2)^2 - x^2) d x = (38)/(35)

Resposta

(overset(-)(x) , overset(-)(y)) = ((5)/(14) , (38)/(35))

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Use o Teorema de Pappus e o resultado do Exercício 39 para calcular o volume do sólido gerado quando a região limitada pelo eixo x e o semicírculo gira em torno da (a) reta y=-a
Como podemos reconhecer se um problema pode ser resolvido utilizando o Teorema de Pappus? Ou seja, quais são as “pistas” e as “incógnitas” que poderiam sugerir uma tal solução? Discuta dois ou três ex
Use o Teorema de Pappus e o fato de que a área de uma elipse com semieixos a e b é π a b para calcular o volume do toro elíptico gerado pela revolução da elipse x - k 2 a 2 + y 2 b 2 = 1 em torno do e
Use um CAS para encontrar a massa e o centro de gravidade da lâmina dada de densidade δ .A lâmina delimitada por y = e x , y = 0 , x = 0 e x = 1 ; δ = 1 e - 1 .
Use um CAS para encontrar a massa e o centro de gravidade da lâmina dada de densidade δ .A lâmina delimitada por y = s e nx , y = 0 , x = 0 e x = π ; δ = 4 .