Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 1.1 - Ex. 55
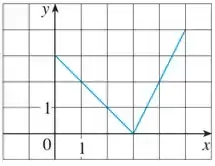
Encontre uma expressão para a função cujo gráfico é a curva dada:
Passo 1
Fala galera, beleza?
A questão quer que encontremos uma expressão para a função em que seu gráfico é dado por:
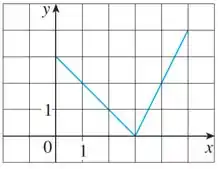
Para resolver essa aqui, devemos verificar que o nosso gráfico é composto por duas retas com comportamentos diferentes (já que uma é mais inclinada que a outra).
Por causa disso, a gente vai quebrar a nossa função, que chamaremos de , em duas partes: a primeira reta e a segunda reta, beleza?
Bora lá!! 😉
Passo 2
Para montar a expressão de qualquer reta, tudo o que precisamos é de dois pontos.
Na primeira reta, vamos pegar os pontos e , enquanto na segunda reta, pegaremos os pontos e , fechou?
Mas você pode pegar quaisquer outros pontos que, no final, tem que dar a mesma resposta ;)
Veja só! 😉
Passo 3
A gente vai montar a expressão referente à primeira reta primeiro. Temos uma expressão que é uma mão na roda quando a gente quer achar a equação de uma reta que é a seguinte:
Nessa expressão, e representam as coordenadas de um ponto da reta, enquanto e os dados do outro ponto.
Vamos chamar de ponto e o de ponto . Olha como nossa expressão vai ficar:
Dando mais uma arrumadinha, a gente vai ter:
Essa vai ser a expressão da nossa primeira reta! Presta atenção em uma coisa: no gráfico, ela só existe no intervalo .
Ou seja, a expressão só vale pra essa condição, ta bom?
Bora prosseguir! 😊
Passo 4
Vamos achar a expressão da outra reta fazendo e . Olha só no que vai dar:
Dando mais uma arrumada, vamos ter:
Pronto, achamos a segunda reta! Pelo gráfico, essa aqui só vale para . Pronto, isso finaliza nossa questão! Nossa vai ser:
Dá uma olhada que, na segunda condição de existência, tem um “” e não um “”.
Isso é só uma questão de notação mesmo (você deve colocar um símbolo em uma condição e o outro símbolo na outra, independente da ordem).
Não vai esquecer disso quando for escrever a sua resposta, combinado? ;)
Entendeu tudo? Responde Aí! 😎
