Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 6.2 - Ex. 7
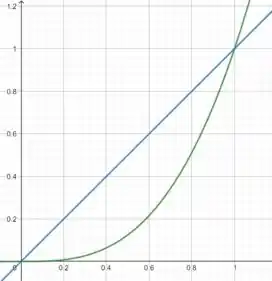
Encontre o volume do sólido obtido pela rotação da região limitada pelas curvas dadas em torno das retas especificadas.
Em torno do eixo .
Passo 1
Eaee, belezinha?? Bom... nessa questão queremos encontrar o volume do sólido gerado ao rotacionar a função apresentada em torno do eixo :
Para e .
Para isso, utilizaremos o conceito de Volume de Sólidos de revolução e as técnicas de integração para calcular o valor desse volume.
Lembrando que seja um sólido que está entre e . Se a área da secção transversal de no plano , passando por e perpendicular ap eixo , é , onde é uma função contínua, então o volume é dado por:
Após encontrar o volume, iremos esboçar graficamente o sólido e a região.
Agora vamos aplicar!! 😉
Passo 2
Se liga! Para calcular o volume, vamos primeiro ter uma noção de como vai ficar o sólido.
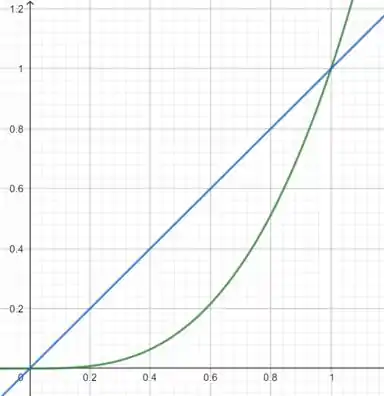
A reta azul representa e a linha verde representa
Passo 3
Agora é seguinte, para calcular o volume, precisamos usar a fórmula do volume dos sólidos de revolução. Como estamos girando em torno do eixo , usaremos:
Onde a área é dada por
Analisando o gráfico, onde a área é justamente a região sombreada.
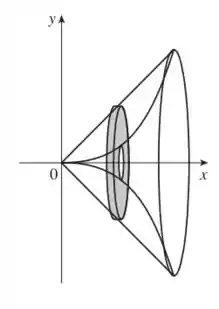
Podemos perceber que o raio externo é
E o interno
Sendo assim, podemos escrever
Passo 4
Agora precisamos calcular a integral.
Como no enunciado foi dito que e podemos perceber pelo gráfico que os pontos de interseção entre a funções são
Podemos definir o intervalo de como
Passo 5
Agora podemos montar a integral e resolvê-la
Podemos jogar o para fora da integral. Assim temos
Enfim, achamos o volume!!
Entendeu direitinho?? Responde aee 😉
Resposta
