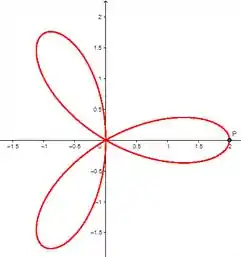
Esboce a curva com a equação dada.

O que a equação representa?

Nas equações polares o representa a distancia do ponto até a origem e o o ângulo do ponto em relação ao eixo horizontal positivo.

Nessa equação não temos um termo constante, e não vai ser tão simples mudar para coordenadas cartesianas, e mesmo assim não seria uma equação que reconheceríamos como algo conhecido, então vamos na raça.

Primeiramente calculamos valores de para alguns valores de :

Vamos calcular para e

Agora precisamos saber como a função se comporta entre esses ângulos, para isso vamos analisar a função .

Como o 2 é só uma constante multiplicando, vamos analisar somente o e no gráfico dobramos todos os valores.

A análise vai ser um pouco complicada, já que temos o 3 como multiplicativo no argumento, teremos que fazer uma análise dando 3 voltas no círculo trigonométrico. Por isso a curva tem três “pétalas”.

Vamos analisar entre os ângulos agora!

Com entre e o argumento do cosseno varia de à , como temos o multiplicativo 3 no argumento, neste intervalo o valor do cosseno varia de à 0, depois vai até e retorna ao .

Utilizando a mesma idéia, para entre e , o argumento do cosseno vai de até , e neste intervalo o valor do cosseno vai de até e depois volta ao e depois vai até .

De entre até o argumento varia de à e o valor do cosseno vai de à depois vai até e retorna ao Finalmente com entre e o argumento varia de a e o valor do cosseno vai de até e então volta ao e por fim vai at�� o .

Bem chatinho né? Mas vamos lá, tá terminando. Neste caso não faz diferença se desconsiderarmos os valores negativos de , porque se você observar nesses pontos é como se a curva sobreposse outra e acaba ficando a mesma coisa.

Desenhando o gráfico fica assim:

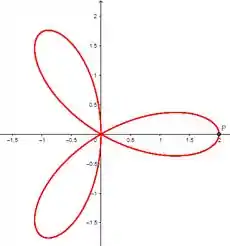
Acabamos!!!